Let me quickly build up some background.
One way to build a hypercube is to take cubes, and start gluing them together, face to face, such that each edge is shared by $3$ cubes. You complete the hypercube with $8$ cubes. This involves rotating cubes in $4$ dimensions, but if you forget about the geometry, you can still do this abstractly.
Separately, lets take a torus that is made from 5 squares, like this:
where you identify opposite sides in the usual way to make a torus.
Now, lets combine these concepts. Let's take these tori and (abstractly?) glue them together, square face to square face, such that each edge is shared by 3 tori. It turns out this only takes $6$ of these tori.
My question is this: where the hypercube lives nicely in $4$-space, is there a nice, familiar, space where this clump of tori lives? Is there a nice way to think about this kind of object?
EDIT:
As requested in the comments, here is a gluing diagram for what I am proposing:
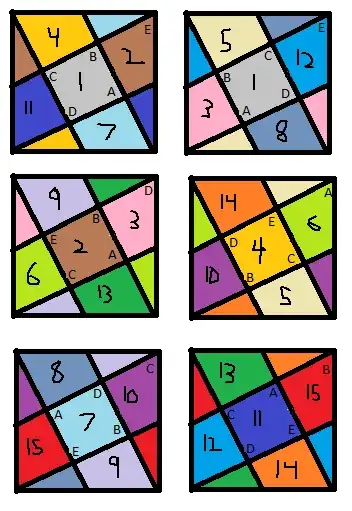
The numbers and colors mean the same thing, they identify square faces to be glued together. The letters correspond to the vertices, so one knows the orientation of the squares to be glued.
