For any given integer $n$, it is known that the Pisano period $\pi(n)$ exists and is finite. There are also plenty of formulas for upper bounds, lower bounds, and exact lengths of $\pi(n)$ under various conditions. What do we know, though, about the sequences themselves? Specifically (and pardon my imprecise notation here), let's say $P_n = \{F_0 \textrm{ mod }n,F_1 \textrm{ mod }n, ...\}$. That is, $P_n$ is the set of all integers in the Fibonnaci sequence modulo $n$ (which is the same as the set of all integers in the first $\pi(n)$ elements of the Fibonnaci sequence modulo $n$, since it just repeats afterwards). I'm curious about the following:
- Is there a formula to determine $P_n$ for any given $n$?
- If not, is there at least a formula to determine $|P_n|$ for any given $n$?
For example, the first $\pi(n)$ elements of the Fibonnaci sequence modulo $n$ where $n=16$ are are $0, 1, 1, 2, 3, 5, 8, 13, 5, 2, 7, 9, 0, 9, 9, 2, 11, 13, 8, 5, 13, 2, 15, 1$. In this case, $P_n = \{0, 1, 2, 3, 5, 7, 8, 9, 11, 13, 15\}$, and $|P_n| = 12$.
A more interesting formulation of the same problem (to me) concerns $\{0, 1, 2, ..., n-1\} - P_n$ and, analogously, $n-|P_n|$. Here, those would be $\{4, 6, 10, 12, 14\}$ and $5$, respectively.
Obviously, all Fibonnaci numbers below $n$ are included in $P_n$. In addition, every sequence seems to end with $2, n-1, 1$, so $n-1$ is included as well. Further analysis, though, may be beyond my modest skills.
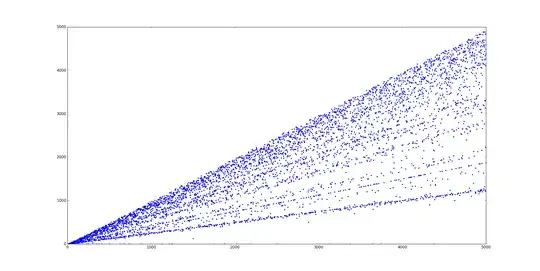
Here are the values of $n-|P_n|$ for $1 < n < 5000$, which seems to follow a similar "banded" pattern as the graph of $\pi(n)$ itself (would link but don't yet have the reputation - it's the first image on the Wikipedia page for the Pisano period, already linked above).