Number of tangent lines to an algebraic curve passing through a given point

Question

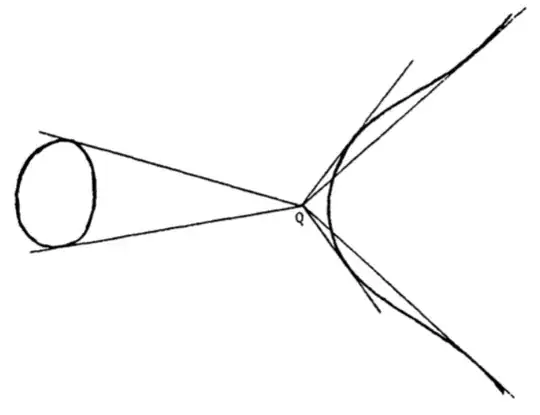
Let $C=V(f)\subset \mathbb{P}^2$ be a smooth plane algebraic curve of degree $d$.

1. For all $x\in \mathbb{P}^2\setminus C$ there are at most $d(d-1)$ tangent lines to $C$ passing through $x$.

2. There exists an $x$ such that we have an equality in the statement above.

For the first part I have tried to do this: After a translation we can assume that $x=(0:0:1)$, then as an arbitrary line passing through $x$ has exactly one intersection with the line at infinity we have an unique parametric representation in the form $l_{(a:b)}=\{(a\mu:b\mu:\lambda); \lambda,\mu \in k\}$ for some $(a:b)\in \mathbb{P}^1$.

Now, $l_{(a:b)}$ is tangent to $C$ $\iff$ one of the equations $f(ax,bx,1)=0$ or $f(a,b,x)=0$ has a multiple root $\iff$ one of the associated discriminants $\Delta_{(a:b)}$ or $\hat{\Delta}_{(a:b)}$ vanished.

If $(a:b)\neq (1:0)$ we can take $b=1$ and studying $P(a)=\Delta_{(a:1)}$ and $Q(a)=\hat{\Delta}_{(a:1)}$ as polynomials in $a$ so it would be enough to prove the following

$\deg(P)+\deg(Q)+\#(\{\Delta_{(1:0)}\}\cap \{0\})+\#(\{\hat{\Delta}_{(1:0)}\}\cap \{0\})\leq d(d-1)$

But I don't know how to compute $\deg(P)$ or $\deg(Q)$ so I don't know hot to continue.

For the second part perhaps I could take $x=(c:0:1)$ and make computations similar to those above to obtain expressions of the form $\Delta_{c,(a:b)}$ and $\hat{\Delta}_{c,(a:b)}$. Then if we define $P^c(a)=\Delta_{c,(a:1)}$ and $Q^c(a)=\hat{\Delta}_{c,(a:1)}$ maybe we can choose $c\in k$ such that $P^c$ and $Q^c$ have different roots and $\Delta_{c,(1:0)},\hat{\Delta}_{c,(1:0)}\neq 0$. Then $\deg(P^c)+\deg(Q^c)$ would be equal to the number of tangent lines, and a good understanding of the first part should give us a way to compute this.

As noticed here assuming Hurwitz's formula this problem is equivalent to Plücker's Formula and that's where my interest comes from.

Answer 1

From Fulton, W. (1984). Introduction to intersection theory in algebraic geometry (No. 54). American Mathematical Soc. p.2:

1.2 Class of a curve (Plücker). An important early application of Bézout's theorem was for the calculation of the class of a plane curve $C$., i.e., the number of tangents to $C$ through a given general point $Q$: Equivalently, the class of $C$ is the degree of the dual curve $C^{\vee}$. If $F(x,y,z)$ is the homogeneous polynomial defining $C$ and $Q=(a:b:c)$, then the polar curve $C_Q$ is defined by $$F_Q(x,y,z)=aF_x+bF_y+cF_z,$$ where $F_x=\frac{\partial F(x,y,z)}{\partial x},F_y,F_z$ are partial derivatives. This is defined so that a nonsingular point $P$ of $C$ is on $C_Q$ exactly when the tangent line to $C$ at $P$ (defined by $xF_x(P)+yF_y(P)+zF_z(P)=0$) passes through $Q$. One checks that $C$ meets $C_Q$ transversally at $P$ if $P$ is not a flex on $C$, so $$\operatorname{class}(C)=\#C\cap C_Q = \deg{C}\deg{C_Q}=n(n-1),$$ if $n$ is the degree of $C$, and $C$ is nonsingular.

If $C$ has singular points, however, they are always on $C\cap C_Q$, so they must contribute. For example, if $P$ is an ordinary node (resp. cusp) and $Q$ is general, then $$i(P,C\cdot C_Q)=2 (\text{resp. } i(P,C\cdot C_Q))=3).$$ This gives the first Plücker formula [50] $$n(n-1)=\operatorname{class}(C)+2\delta+3\kappa,$$ if $C$ has degree $n$, $\delta$ ordinary nodes, $\kappa$ ordinary cusps, and no other singularities.

[50] Plücker, J. Solution d'une question fondamentale concernant la théorie générale des courbes.. Journal für die reine und angewandte Mathematik, 1834(12), pp. 105-108. doi:10.1515/crll.1834.12.105