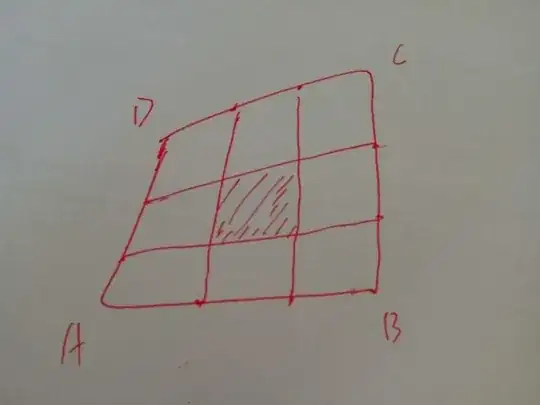
This is a problem which baffled me for years. Many possibly know the solution. See the figure below. $ABCD $ is some arbitrary quadrilateral. Each side is divided evenly into three parts. It is asserted that the quadrilateral shaded has an area 1/9 of that of the $ABCD$.
My first idea was using affine or projective geometry. But the affine transform cannot transform $ABCD$ into a square. The projective transform can, but it does not preserve the ratio (no longer evenly divided).
So, could you provide the solution for me?