I found a nice proof of the linear regression formulas by using physical springs in Mark Levi's Mathematical Mechanic on page 43.
Linear Regression (The Best Fit) via Springs Imagine a collection of data points $(x_i, y_i)$ in the plane. We are asked to find the straight line $y = ax +b$ that best fits this set of data. What does “best” mean? To answer this, for each $x_i$ we think of $y = ax_i+b$ as the predicted value, while $y_i$ is the observed or measured value. The mismatch between these two values is $y_i − (ax_i + b)$, called the error (figure 3.4). “Best line” here means the line for which the sum of squares of the errors is minimal. The precise formulation of the problem of best fit, also called the problem of linear regression, follows.
Problem Given $N$ data points $(x_k , y_k)$ in the plane, find the straight line $y = ax + b$ which fits these data best in the sense of minimizing the sum of squares of errors $$ S(a, b) = \sum_{i=1}^N{(y_i-(ax_i+b))^2} \tag{3.1} $$
The unknowns in this problem are the slope $a$ and the intercept $b$ of the “best” straight line. The standard method to find the minimum of (3.1) is to set the partial derivatives with respect to $a$ and $b$ to zero. Here is a mechanical shortcut to the answer.
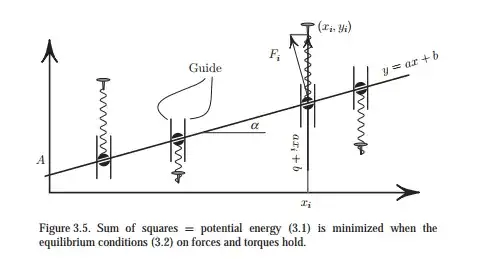
Solution The unknown straight line is to be imagined as a rigid rod (figure 3.5). Let us pass the rod through frictionless sleeves constrained to vertical lines $x = x_i$ by frictionless guides. Each sleeve is connected to a nail (hammered into a data point) by a zero-length spring. Let us take Hooke’s constant to equal, so that the potential energy of each spring is simply the square of its length. The sum (3.1) has now acquired a physical meaning of potential energy!
If the sum of squares is minimal, then the potential energy of our mechanical system is minimal, and consequently the rod is in equilibrium. The only forces the rod “feels” are the normal reactions $F_i$ from the sleeves; the sum of these forces vanishes, as does the sum of their torques relative to the point of intercept $A$: $$ \sum_{i=1}^NF_i = 0 \tag{3.2} $$ $$ \sum_{i=1}^Nd_iF_i = 0 \tag{3.2} $$ where $d_i$ is the distance from the intercept to the sleeve. Note that $d_i \cos{\alpha} = x_i$ . Now to get an expression for $F_i$ , consider the balance of forces upon the sleeve. The sleeve feels
(i) the reaction force $−F_i$ from the rod
(ii) the pull of the spring, $y_i − (ax_i +b)$, and
(iii) the reaction from the guide in the $X$ direction.
Only two of these forces have nonzero $Y$ components, and they are in balance: $F_i \cos{\alpha} = y_i − (ax_i + b)$. Using these expressions for $d_i$ and $F_i$ in (3.2) we obtain
$$ \sum{Y}-a\sum{X}-Nb = 0 \tag{3.3} $$ $$ \sum{XY-a\sum{x^2}-b\sum{X}} =0 \tag{3.3} $$
This is a system of two equations with two unknowns a and b which, when solved, produces the “best” slope and intercept.
Note that the same result (3.3) can be obtained directly by setting partial derivatives of the error in (3.1) to zero.
The images (referenced in the above paragraph) and some footers can be seen by following the second, third and first link respectively.
My question
Is this a valid mathematical proof or just a nice new insight? Is there any obvious logical fallacy here?