0

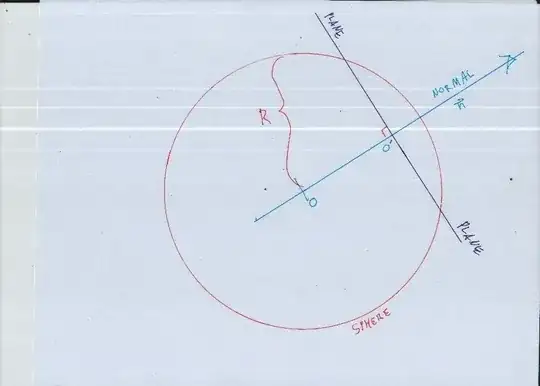
How do i describe the circle resulting from the intersection of the plane $ax+by+cz+d=0$ and the sphere centred at $O(X_0,Y_0,Z_0)$ with radius $R$

I found that the plane-sphere distance $\rho$ is less than the radius of the sphere so a circle is formed I also found from my diagram that the radius $r$ of my circle follows $r = \sqrt{R^2-{\rho}^2}$ But how do I go about finding the coordinates of the centre

Let $\vec{n}$ be normal to the plane, $O'$ the centre of the circle I thought of saying $\vec{n} \times \vec{OO'} = \vec{0}$ Since $\vec{OO'}$ is parallel to $\vec{n}$

Thanks in advance

arsene stein
  • 409

1 Answers1

1

The centre of your circle is the intersection of the plane with the line that passes through the centre of the sphere and is perpendicular to the plane.

enter image description here

Will Jagy
  • 146,052
  • If I got you right I should write the parametric equation of the line that passes through the centre of the sphere and is parallel to the normal of the plane , substitute x,y,z in the plane and solve for the parameter? – arsene stein Jul 22 '17 at 20:05
  • @arsenestein I added a picture – Will Jagy Jul 22 '17 at 20:19