Pi, the Lemniscatic elliptic functions, and the Dixonian elliptic functions

Question

$n=2$

Circle: $x^2+y^2=c^2$. We all know the role of $\pi$ in the circle and the trigonometric functions,

$$\pi_2 = \color{brown}{B\big(\tfrac12,\tfrac12\big)}=3.1415\dots$$

with the beta function $B(x,y)$ and circumference for $D=1$

$$C=\pi_2 = 3.1415\dots$$

$n=4$

Lemniscate: $(x^2+y^2)^2=2c^2(x^2-y^2)$ (or $r^2=2c^2\cos2\theta$ in polar form):

$\hskip1.4in$

The lemniscate constant $L$ plays an analogous role to $\pi$,

$$L =\frac{\color{brown}{B\big(\tfrac14,\tfrac14\big)}}{2\sqrt2}= \frac{B\big(\tfrac12,\tfrac14\big)}{2}= \frac{\sqrt\pi\,\Gamma\big(\tfrac14\big)}{2\Gamma\big(\tfrac34\big)}=\frac{\Gamma^2\big(\tfrac14\big)}{2\sqrt{2\pi}}=2.622057\dots$$

and if $c=1$,

$$\text{Arclength} = 2L = 5.2441\dots$$

The minimal half period $\omega_1$ of the lemniscatic elliptic functions is,

$$\omega_1=\frac{L}{\sqrt2}=\frac{\Gamma^2\big(\tfrac14\big)}{4\sqrt{\pi}}$$

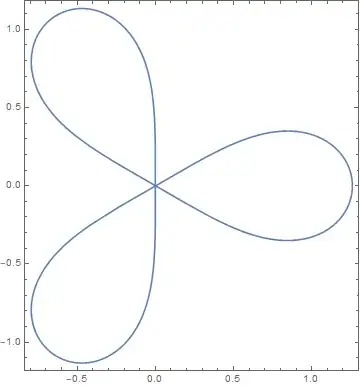
$n=3$

Object?: ($3$rd or $6$th deg poly?) However, it seems we missed a step,

$$\pi_3 = \color{brown}{B\big(\tfrac13,\tfrac13\big)}=2^{1/3}\,B\big(\tfrac12,\tfrac13\big) =\frac{\Gamma^2\big(\tfrac13\big)}{\Gamma\big(\tfrac23\big)}=\frac{\sqrt{3}\,\Gamma^3\big(\tfrac13\big)}{2\pi}=5.29991\dots$$

which conveniently is the fundamental constant of the Dixonian elliptic functions.

Q: So does the constant $\pi_3$ play an analogous role for some geometric object akin to the circle and lemniscate?

Edit: To clarify (courtesy of reuns' comments): to know the arc length of a circle you need $\pi_2$. For a lemniscate, you need $L$. So is there a simple geometric object where to know its arc length you need $\pi_3$?

Answer 1

Langer and Singer, in their paper, present the trefoil, which has the Cartesian equation

$$(x^2+y^2)^3=2(x^3-3xy^2)$$

and polar equation $r^3=2\cos3\theta$:

$\hskip1.3in$

Using the normal formula for determining the arclength of a polar curve, its total arclength comes out to

$$\text{Arclength} =\sqrt{3}\,\pi_3=9.179724\dots$$

Additionally, they also present a unit-speed parametrization in terms of the Dixon functions. Letting $\sigma=\operatorname{sm}\dfrac{s}{\sqrt3}$ and $\chi=\operatorname{cm}\dfrac{s}{\sqrt3}$, we have the arclength parametrization

$$f(s)=\begin{pmatrix}\dfrac{3\chi\sigma^4}{2(\chi^3\sigma^3-1)}\\\dfrac{\sqrt{3}\chi\sigma(1+\chi^3)}{2(1-\chi^3\sigma^3)}\end{pmatrix}$$

See this related paper as well.

Answer 2

To make my comments clear:

• Look at the differential equation $g'(x)^2 = 1-g(x)^n$. The solution depends only on the initial conditions $(g(0),g'(0))$. The initial condition $g(0) = 0$ implies $g'(0) \pm 1$ and two possible real solutions. If for some $x_0 \ne 0$, then $g$ is periodic with period $x_0$ or $2 x_0$.

• Let $$F_n(z) = \int_0^z \frac{ds}{\sqrt{1-s^n}}, \quad G_n = F_n^{-1}, \quad G_n'(z) = \frac{1}{F_n'(G_n(z))}, \quad G_n'(z)^2 = 1- G_n(z)^n$$ $G_n(x)$ is real for $x$ real and $G_n(0)=0$; thus, it satisfies the preceding differential equation.

• Let $$\omega_n = \int_{\gamma} \frac{ds}{\sqrt{1-s^n}}$$ where the contour $\gamma$ goes from $s=0$, encloses the branch point $s=1$ in a clockwise direction and goes back to $s=0$, with the branch of $\sqrt{1-s^n}$ chosen such that it stays analytic on this path. Then with a change of variable $s = G_n(u)$, we obtain $$\omega_n= \int_{0}^{x_0} \frac{G_n'(u)}{\sqrt{1-G_n(u)^n}}du = x_0$$ Where $G_n(x_0) = G_n(0) = 0$ and hence $G_n$ is $2 x_0$-periodic. But choosing the branch of $\sqrt{1-s^n}$ correctly, we have the other expression $$2\omega_n = 2\int_0^1+\int_1^0 \frac{ds}{\sqrt{1-s^n}} = 4 \int_0^1 \frac{dt}{\sqrt{1-t^n}}=4 \int_0^1 \frac{v^{1/n-1}dv}{n\sqrt{1-v}}= \frac{4}{n} B(1/2,1/n)$$

• $z \mapsto (G_n(z),G_n'(z))$ parameterizes the curve $\{ (x,y) \in \mathbb{C}^2, y^2 = 1-x^n\}$ and the period $2\omega_n$ is the arc-length (?) of $\{ (x,y) \in \mathbb{R}^2, y^2 = 1-x^n\}$ in those coordinates.