The title of your question is misleading. I suppose you are interesting in the language of all words not containing $11$ as a substring. More generally, given a word $u$, the set of words containing $u$ as a substring is the language
$$
L(u) = \Sigma^*u\Sigma^*
$$
Therefore, the set of words not containing $u$ as a substring is the complement of $L(u)$. If you want a regular expression for this language, you can proceed as follows
- First compute the minimal DFA of $L(u)$ (this automaton has $|u| + 1$ states).
- Compute the minimal DFA of its complement (just swap the final states and the non final ones).
- Compute a regular expression from the resulting DFA.
For your example, $u = 11$, the minimal automaton of $L(11)$ is
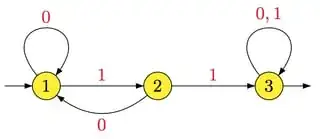
and the minimal automaton of its complement is
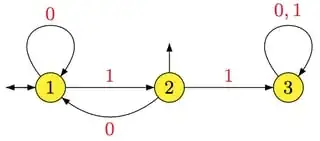
It is now easy to get a regular expression for the language accepted by this automaton: $(0 + 10)^*(\varepsilon + 1)$.

