0

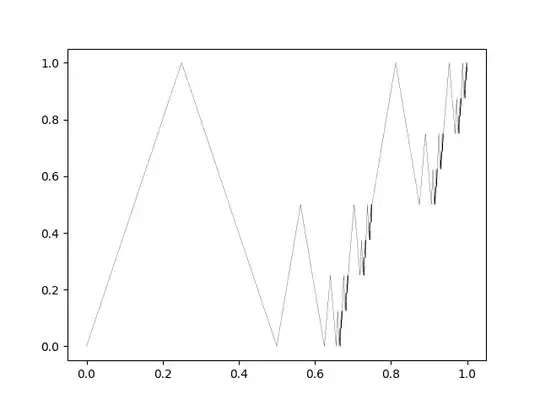
Say that $p$ is a bumpy point if there is a collection of "bumps" limiting to it:

enter image description here

A collection of these bumps and their limit point can lie on any horizontal line (except obviously for the top line $[0,1]\times \{1\}$).

Question: If $f:[0,1]\to [0,1]$ is continuous, then must number of bumpy points on the graph of $f$ be countable?

Easier Question: Does there exist a horizontal line with no bumpy points (other than the top line)?

Note: I do not require that the "bumps" be semi-circles. They just have to be arcs beginning and ending at the same horizontal line as their limit point, and lie completely above that horizontal line.

Forever Mozart
  • 9,534

2 Answers2

1

No, there can be uncountably many bumpy points.

Consider the function $f$ defined as the uniform limit of the functions $f_n\colon[0,1]\mapsto [0,1]$ defined by $$ \begin{align} f_0(x)&=x\\ f_{n+1}(x)&=\begin{cases} 4x & (0\leq x \leq \tfrac 1 4)\\ 1-4(x-\tfrac 1 4) & (\tfrac 1 4\leq x \leq \tfrac 2 4)\\ \tfrac 1 2 f_n(4(x-\tfrac 2 4)) & (\tfrac 2 4\leq t \leq \tfrac 3 4)\\ \tfrac 1 2 + \tfrac 1 2 f_n(4(x-\tfrac 3 4)) & (\tfrac 3 4\leq t \leq 1).\\ \end{cases} \end{align}$$

bumpy function

For each $k\geq 0$ and each choice of binary digits $b_1,\cdots,b_k\in\{0,1\}$, this function has separate bumps going from y-coordinate $\sum_{i=1}^k b_i 2^{-i}$ to $2^{-k} + \sum_{i=1}^k b_i 2^{-i}$ and back. So any y-coordinate in $[0,1)$ intersects infinitely many bumps. This also answers the "easier question" in the negative.

Colin McQuillan
  • 6,747
  • Maybe this should be a new question, but what if we require $f$ to be differentiable (or even continuously differentiable)? Do you know a quick answer to that? – Forever Mozart Jun 26 '17 at 00:13
  • I don't have a quick answer to that. I just know Sard's theorem implies that a continuously differentiable function has a horizontal line with no bumpy point. – Colin McQuillan Jun 26 '17 at 05:07
  • @ForeverMozart: I think the situation is as follows. If we define $C(f)$ to be the projection of the bumpy points of $f$ to the y-axis, then: if $f$ is differentiable then $C(f)$ is a null set (can be shown by a covering argument as in George Lowther's equation (1) here https://math.stackexchange.com/a/59115/3643 and noting that if a derivative exists at a bumpy point it must be zero), and given any null set $Y$ there is a smooth $f$ such that $C(f)=Y$ (this can be shown by a recursive construction a bit like in my answer). – Colin McQuillan Jun 27 '17 at 20:36
  • Okay great. One last question: What if I allow the "bumps" to have height that is bounded below by some positive number? Does the projection of the points still have measure $0$? Actually in this case $f$ would have a vertical tangent... – Forever Mozart Jul 02 '17 at 17:22
  • @ForeverMozart: yeah, the bumpy points would then be essential discontinuities, so won't exist for continuous $f$ – Colin McQuillan Jul 02 '17 at 17:57
1

Hint: Take the well known continuous function, but no where differentiable

Red shoes
  • 7,184