Number of circles with turning points of an arc

Question

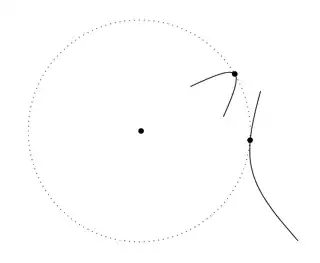
Let $A$ be an arc in the plane (so there is a homeomorphism $h:[0,1]\to A\subseteq \mathbb R ^2$).

Assume that $h(0)$ is the origin $o$ in the plane.

Say that a point $p\in A$ is a turning point if there is a neighborhood $U:=h[(a,b)]$ of $p$ such that $$\{p\}=U\cap B(o,\epsilon),$$ and either $U\subseteq \overline{B(o,\epsilon)}$ or $U\subseteq \mathbb R ^2\setminus B(o,\epsilon)$, where $\epsilon=d(o,p)$.

Let $T$ be the set of turning points in $A$.

Question: Is $\{\epsilon>0:T\cap \partial B(o,\epsilon)\neq\varnothing\}$ necessarily a countable set?

Easier Question: Does there exists $\epsilon>0$ such that $A\cap \partial B(o,\epsilon)\neq \varnothing$ and $T\cap \partial B(o,\epsilon)=\varnothing$?

Do you mean for $h(0)$ to be the origin? That seems like it contradicts your picture. — Rocket Man, Jun 24 '17 at 03:29
$h(0)$ is the center of the circle in the picture, which you can think of as the origin in the plane (technically there should be a line leaving it) — Forever Mozart, Jun 24 '17 at 03:30
I don't suppose that $h$ is known to be continuously differentiable? — Chris Culter, Jun 24 '17 at 05:08

score 1 · Accepted Answer · answered Jun 24 '17 at 05:20

1

In fact, $T$ itself is countable! Define $f:[0,1]\to\mathbb R$ by $f(t)=|h(t)|$. Then we can identify $T$ with the strict local extrema of $f$. But there are only countably many of those, since each minimum or maximum can be uniquely bounded by a pair of rational numbers. (For details on this step, see: Does there exist a continuous function from [0,1] to R that has uncountably many local maxima?)

answered Jun 24 '17 at 05:20

Chris Culter

27,415

oh, how clever! – Forever Mozart Jun 24 '17 at 17:29

Number of circles with turning points of an arc

1 Answers1