Derivative of $\|X-\alpha Y\|_2$ with respect to $\alpha$.

Question

Let $X$ and $Y$ be operators on a real or complex Hilbert space $\mathcal{H}$ and $f(\alpha) = \|X - \alpha Y\|_2$ where $\alpha$ is real and $\|A\|_2 = \sigma_{\mathsf{max}}(A)$ is the $\ell^2$-induced operator norm. What is $\frac{df}{d\alpha}$?

Even if the function is not differentiable everywhere, $f$ is convex in which case a sub-gradient will suffice.

Also, if it helps we can assume $X=I$ and $Y$ is positive definite but I'd rather see a more general result. Also considering $f^2$ instead of $f$ is also fine if that helps.

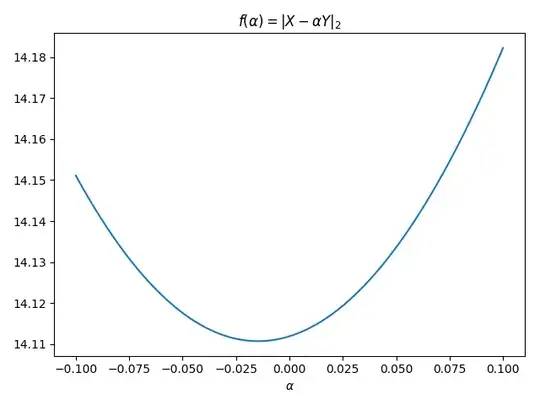
Plots of $f$: I ran two simple numerical examples which might be enlightening. In the following plot 1, $X = I\in M_{50}(\mathbb{R})$ and $Y = Z^\mathsf{T}Z + I$ where $Z_{ij}\sim\mathcal{N}(0,1)$ is normally distributed. As we can see, the plot seems piecewise linear.

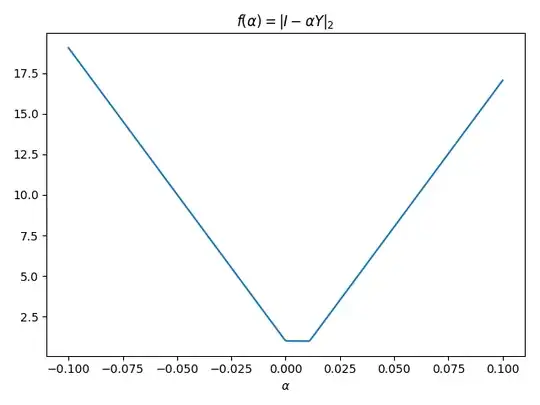
In the next plot 2, we take $X_{ij}\sim\mathcal{N}(0,1) - I \in M_{50}(\mathbb{R})$ and $Y_{ij}\sim\mathcal{N}(0,1)$. Note that neither $X$ nor $Y$ are symmetric. This example looks differentiable and practically quadratic.

Answer 1

There's at least a subset of cases here where we can do this. Note that for any norm $\|\cdot\|$, $$\|W\| = \sup_{\|Z\|_* \leq 1} \langle W, Z \rangle$$ where $\|\cdot\|_*$ is the dual norm. For the case of the matrix spectral norm, the dual norm is the nuclear norm (the sum of the singular values). Any maximizing value of $Z$ above is a subgradient of the norm at that point. That is, let $Z^*$ be any point satisfying $$\|Z\|_* = 1, \quad \langle W, Z \rangle = \|W\|.$$ then $$\|W + \delta W\| \geq \langle W + \delta W, Z^* \rangle = \langle W, Z^* \rangle + \langle \delta W, Z^* \rangle = \|W\| + \langle Z^*, \delta W \rangle$$ so $Z^* \in \partial \|W\|$. For the matrix spectral norm, valid values of $Z^*$ are readily obtained: if $W=U\Sigma V = \sum_i \sigma_i u_i v_i^H$ is the SVD of $W$, then $$\partial \|W\|_2 = \mathop{\textrm{Conv}}\{u_iv_i^H\,|\,\sigma_i=1\}.$$

Now in the case where $W=X-\alpha Y$ and $\delta W=-\alpha Y$, then, we have $$\|X-(\alpha+\delta \alpha)Y\| \geq \|X-\alpha Y\| + \langle Z^*, -\delta \alpha Y\rangle = \|X-\alpha Y\| - \delta\alpha \langle Z^*, Y \rangle$$ So $-\langle Z^*, Y \rangle \in \partial f(\alpha)$. For the matrix spectral norm, the subgradient can be obtained using the above SVD approach on $X-\alpha Y$ to obtain values of $Z^*$. So we have $$\partial f(\alpha) \subseteq \mathop{\textrm{Conv}}\{-\Re{v_i^TZu_i}\,|\,Z\in\partial \|X-\alpha Y\|_2\}.$$

Answer 2

$ \def\R#1{{\mathbb R}^{#1}} \def\a{\alpha} \def\s{\sigma} \def\k{\otimes} \def\h{\odot} \def\t{\times} \def\o{{\tt1}} \def\bR#1{\big(#1\big)} \def\BR#1{\Big[#1\Big]} \def\LR#1{\left(#1\right)} \def\op#1{\operatorname{#1}} \def\vc#1{\op{vec}\LR{#1}} \def\rank#1{\op{rank}\LR{#1}} \def\trace#1{\op{Tr}\LR{#1}} \def\frob#1{\left\| #1 \right\|_F} \def\qiq{\quad\implies\quad} \def\mt{\mapsto} \def\p{\partial} \def\grad#1#2{\frac{\p #1}{\p #2}} \def\deriv#1#2{\frac{d #1}{d #2}} \def\c#1{\color{red}{#1}} \def\CLR#1{\c{\LR{#1}}} $Given the Singular Value Decomposition of a matrix $A\in\R{m\t n},\;\,r=\rank A$ $$\eqalign{ A &= \sum_{k=\o}^r \s_k\,u_k\,v_k^T \qquad&{\rm where}\;\; \s_\o\gt\s_2\ge\ldots\ge\s_r\gt0 \\ \s_\o &= \|A\|_2 \quad&\{{\rm Spectral\ norm}\} \\ }$$ then from this post (and this one) the gradient of the Spectral norm (wrt $A$) is $$\eqalign{ \grad{\s_\o}{A} &= u_\o v^T_\o \qiq d\s_\o = u_\o^T\,\c{dA}\:v_\o \\ }$$ Substituting $\,A=\bR{Y\a-X}\,$ yields the desired derivative $$\eqalign{ d\s_\o &= u_\o^T\CLR{Yd\a}v_\o \qiq \deriv{\s_\o}{\a} &= u_\o^TYv_\o \\ }$$