Probability of a survivor in chick-pecking tournament

Question

This is a follow up to this question: Suppose that $n$ chicks are arranged in a circle. Every chick randomly pecks either the chick to their right or the chick to their left. By the other question, the expected number of unpecked chicks is $n/4$. Instead of ending there, make a tournament out of it. Remove the pecked chicks from the circle and repeat the experiment with the remaining chicks. Iterate as long as possible. It is easy to see that the process ends with either $0$ or $1$ remaining chick.

Question: Let $p(n)$ denote the probability that the process ends with $1$ chick. What can be said about $\lim_{n \rightarrow \infty}p(n)$?

The following graph shows the result of Monte Carlo simulations which estimate $p(n)$ for all $n$ in the range $1$ to $1000$ (and using $1000$ tournaments for each $n$).

The wave-like nature of the graph is interesting. To get a better handle on it, we need the exact probabilities. The following is based on a nice formula by @6005 in the comments to this answer to the other question: $p(0) = 0$ and $p(1) = 1$. For any $n \geq 2$ we have:

$$p(n) = \begin{cases} \sum_{k=0}^\frac{n}{2} \left(\frac{\binom{n}{2k} + (-1)^k \binom{n/2}{k}}{2^{n-1}}\right) p(k) & \text{if $n$ is even} \\ \sum_{k=0}^\frac{n-1}{2} \left(\frac{\binom{n}{2k}}{2^{n-1}}\right)p(k) & \text{otherwise}. \end{cases} $$

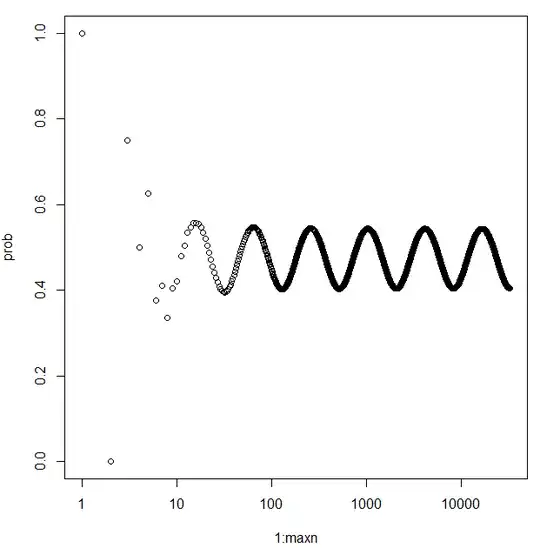
The following shows the graph of $p(n)$ from $n=1$ to $1000$:

The local maxima and minima appear approximately at powers of $2$ (sometimes shifted by $1$). The maxima are at powers of $2$ which are also powers of $4$ and the minima at the other powers of $2$ (hence of the form $2 \cdot 4^k$). This is somewhat intuitive given that the expected number of survisors in a single round is $\frac{n}{4}$. Furthermore, this expected value is also the most likely value (in the case that $n$ is a multiple of $4$). For example if you start with $128$, the first round could be expected to get you to $32$, the next round to $8$, from thence to $2$, which prompty peck each other, leaving you with $0$. This is a hueristic way of reasoning that becomes somewhat less plausible with each factor of $4$.

So the question: Does $\lim_{n\rightarrow \infty} p(n)$ exist, and, if so, to what?

My conjecture is that the observed oscillations get damped in the limit, and that the resulting limit is $0.5$, but I do not know how to compute such limits.

Answer 1

As an expansion of my comment, on an empirical basis I suspect your conjecture may be false, from looking up to $2^{15}=32768$

You seem to have used R for your graphs, so here is my attempt:

c2a <- function(n,k){ exp( lchoose(n,2*k)-(n-1)*log(2) )} 
c2b <- function(n,k){ (-1)^k * exp( lchoose(n/2,k)-(n-1)*log(2) )} 

maxn <- 2^15

prob <- 1
for (n in 2:maxn){
  if (n %% 2 == 0){
    prob [n] <- sum( (c2a(n,1:(n/2)) + c2b(n,1:(n/2))) *
                prob[1:(n/2)] )
    }else{
    prob [n] <- sum( (c2a(n,1:((n-1)/2))) * 
                prob[1:((n-1)/2)] )
    }
  } 

A graph with a log scale looks like

plot(1:maxn, prob, log="x")

and looking at the values at powers of $2$ suggests that the peaks and troughs may have separate limits

> prob[4^(1:7)]
[1] 0.5000000 0.5571170 0.5468982 0.5442833 0.5436387 0.5434781 0.5434380
> prob[2*4^(1:7)]
[1] 0.3359375 0.3950479 0.4016141 0.4031632 0.4035449 0.4036400 0.4036638

while taking a weighted average of the probabilities across a cycle from $m$ through to $4m-1$ suggests a central figure something like $0.475$, which is marginally more than the average of the apparent limits for powers of $2$

wav <- numeric()
for (m in 1:(maxn/4)){
  wav[m] <- sum(prob[m:(4*m-1)]/(m:(4*m-1))) / sum(1/(m:(4*m-1)))
  }
plot(1:(maxn/4), wav, log="x", ylim=c(0.474, 0.476))