Firing a projectile over a circular obstacle.

Question

I want to fire a projectile in gravity over an obstacle. The obstacle is bounded by a circle of known radius $r$, resting on the ground (so that its center is $r$ above the $y=0$ plane).

I will be firing from zero height; I am free to choose my distance $d$ from the obstacle, and the vertical velocity $v_y$ with which it is fired.

The horizontal velocity $v_x$ is fixed.

Clearly there are many solutions where the projectile sails far over the obstacle. How can I find a minimal solution (or set of solutions), where the projectile just barely skims the bounds of the obstacle at one or more points? I imagine there exist values for all of the parameters for which the resulting maximal height of the projectile equals $2r$, touching the circle at the very top. But I am also curious about solutions where the projectile grazes the circle along the sides (once on the way up and once again on the way back down).

(Ignore air resistance and other such factors.)

Answer 1

Hint: Having the horizontal velocity fixed makes the problem simpler. You can't guarantee to graze the top. The minimum energy approach will be one that grazes the circle twice, once on the way up and once on the way down. That forces the path to be symmetric around the vertical axis of the circle, so make that $x=0$. Let $v_y$ be the vertical velocity at launch. If we then take the origin of time to be $t=0$ when $x=0$ we have $y(0)=\frac {v_y^2}{2g}$ and $y(t)=\frac {v_y^2}{2g}-\frac 12gt^2, x(t)=v_xt$ Write the equations for this to be tangent to your circle and you are done. It would be interesting to find the minimum $v_x$ that makes this possible, which grazes the top as well as the other two points.

Answer 2

This solution considers the case where the projectile touches the circle at the very top only.

Assuming no constraints on launch velocity:

The equation of the trajectory of the projectile is a parabola whose equation is $$y-2r=-\frac {2r}{d^2}\big(x-d\big)^2$$ Differentiating wrt $x$ gives $$\begin{align} \frac {dy}{dx}&=-\frac {4r}{d^2}(x-d)\\ \frac {d^2y}{dx^2}&=-\frac {4r}{d^2} \end{align}$$ The radius of curvature at the vertex $V(d,2r)$ of the parabola is given by $$R=\frac {\left[1+\left(\frac {dy}{dx}\right)^2\right]^\frac 32}{\bigg|\frac{d^2y}{dx^2}\bigg|}=\frac {d^2}{4r}\quad\text{at $V$}$$ For the projectile to touch the circle only once at $V$, we require $R\ge r$ or $\frac Rr \ge 1$, i.e. $$\frac {d^2}{4r^2}\ge 1\\ \color{red}{d\ge 2r}$$

Incorporate constraints on launch velocity (i.e. $V_x=$ constant) to determine conditions for which the trajectory is the same as that given above.

The launch angle is $\theta$ where $\tan \theta=\frac {4r}d$. Hence $V_y=V_x\cdot \frac {4r}d$.

After some standard algebraic and kinematic manipulation we find that this requires

$$\color{red}{V_x=\frac d{2r}\sqrt{gr}}$$ Let $\dfrac d{2r}=\mu$ ($\mu\ge 1$), i.e. $d=2\mu r$. Hence $$V_x=\mu\sqrt{gr}\\ \mu=\frac{V_x}{\sqrt{gr}}$$.

Since $V_x, r$ are fixed (given), we have to first test to see if $\mu\ge 1$. If so, then we proceed to determine $d, V_x$ per formulas given above. If not, then there is no solution.

---

(added 27 May 2018)

See also the solution here.

Answer 3

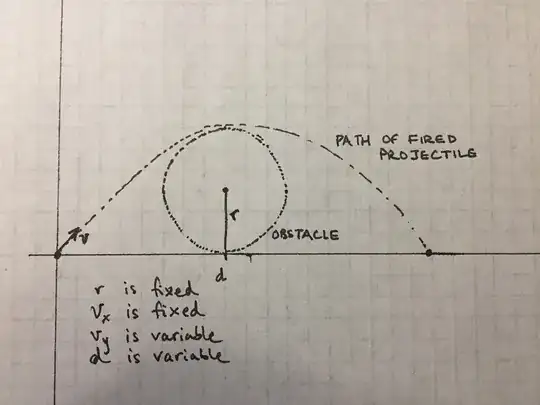
I think I finally have a solution for all cases, thanks to the guidance from the other answers. To simplify the math, recenter the problem so the center of the circle is at the origin. We can fix the results afterwards to fit the original problem. Start with a general parabola and its slope:

$$\begin{align} y&=-ax^2+c \tag{1}\label{1} \\ \frac{dy}{dx}&=-2ax \end{align}$$

And the circle and its slope:

$$\begin{align} y&=\sqrt{r^2-x^2} \tag{2}\label{2} \\ \frac{dy}{dx}&=\frac{-x}{\sqrt{r^2-x^2}} \end{align}$$

If the two curves touch but do not cross, it must happen in the range $0 \le x < r$, because at $x=r$, the slope of the circle is undefined (where our parabola's never is), and after that the circle has no value. Similarly, we can say the range for $y$ is $0 \le y \le r$.

At the point of intersection, the parabola and the circle are tangent to one another (their slopes are equal), so:

$$\begin{align} -2ax&=\frac{-x}{\sqrt{r^2-x^2}}\\ \Rightarrow x&=\sqrt{r^2 - \frac{1}{4a^2}} \end{align}$$

Substituting for $x$ in $\eqref{2}$ yields:

$$y=\frac{1}{2a}$$

Now considering our upper bounds on $y$, we can say:

$$\begin{align} \frac{1}{2a} & \le r\\ \Rightarrow a & \ge \frac{1}{2r} \end{align}$$

Now to get the parabola in terms of velocities and gravity, combine the $x(t)$ and $y(t)$ representations (not shown) to get:

$$y=-\frac{g}{2v_x^2}x^2+\frac{v_y^2}{2g}$$

By comparison to $\eqref{1}$, we can say:

$$a=\frac{g}{2v_x^2}, c=\frac{v_y^2}{2g}$$

And since we have a bounds on $a$, we can conclude:

$$\begin{align} \frac{g}{2v_x^2} & \ge \frac{1}{2r} \\ \Rightarrow v_x & \le \sqrt{rg} \end{align}$$

This constraint defines a set of minimal solutions for a parabola which grazes the bounds of the circle without falling inside it, nor passing clear over it. (There is also a set of solutions which touch the circle at its apex ($x=0,y=r$) but which are "wider" than necessary.)

If $v_x=\sqrt{rg}$, the solution will touch the top of the circle with the minimum possible $v_y$. If $v_x \lt \sqrt{rg}$ (while still greater than zero, of course), the solution will touch the circle twice, once going up and once going down, and arc over the top of the circle in between.

Knowing that, we can get back to solving for $v_y$. Substituting $x$ and $y$ found above into $\eqref{1}$ yields:

$$c=\frac{4a^2r^2+1}{4a}$$

Now substitute $c$ and $a$:

$$v_y=\sqrt{ \frac{g^2r^2}{v_x^2} + v_x^2 }$$

But because we re-centered the problem, what this really gives us is our desired $v_y$ at the circle's midpoint (not from our launch point). Correcting for this is the relatively simple exercise of using the time-domain functions to find the time $t$ at which $y(t)=-r$ and then the velocity at that time.