If $X=(x_1, \ldots, x_n) \in \mathbb{R}^n$, then $x$ is on the unit sphere, if $\lVert X \rVert_{2}=\sqrt{x_1^2+\ldots+x_n^2}=1$.
Now how can I write a proper definition of the uniform distribution on the unit sphere? I was checking the internet for a definition of it but couldn't find a single one
Use the surface measure on the unit sphere (see, for example, Section 2.7 in Folland's Real Analysis 2e). Then, the uniform distribution is given by the surface measure divided by the measure of the whole unit sphere.
To be precise, Theorem 2.49 in Folland tells you theres a unique Borel measure $\sigma$ on the unit sphere $S^{n-1} = \{x \in \mathbb{R}^n: \lVert x\rVert_2 = 1\}$ such that for every non-negative Borel measurable function $f$ on $\mathbb{R}^n$, $$\int_{\mathbb{R}^n} f(x) dx = \int_0^\infty \int_{S^{n-1}} f(r x') r^{n-1} d \sigma(x') dr.$$
This is basically just using Polar coordinates, and and you're concerned with the part which isn't the radius $r$ (so, the angle portions, which are in $\sigma$).
Then, you can define the uniform distribution by the measure $\frac{\sigma}{\sigma(S^{n-1})}$. You'll have $\sigma(S^{n-1}) = \frac{2 \pi^{n/2}}{\Gamma(n/2)}$.
If you're going to write something though, its perfectly clear to just say "Let $\sigma$ be the probability measure associated with the uniform distribution on the sphere $S^{n-1}$". And its clear that when you take an expectation of a RV with this distribution, you're taking it with respect to a scaled version of the surface area.
It depends somewhat upon your purpose.
If for example, you want to uniformly generate a collection of points on a unit sphere you could use the direction cosines $\alpha,\,\beta,\,\gamma$.
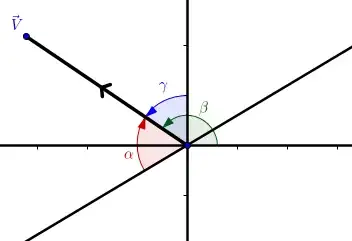
These are not independent, however, since
$$\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$$
So you could identify each unit vector $\vec{V}\in\mathbb{R}^3$ with a triplet $(\alpha,\beta,n)$ where $\alpha$ and $\beta$ are selected uniformly from $[0,\pi]$ and $n$ is selected uniformly from $\{-1,1\}$ so that
$$ \gamma= \frac{\pi}{2}+n\left(\frac{\pi}{2}-\cos^{-1}(1-\cos^2\alpha-\cos^2\beta)\right)$$ and resulting in a probability density function
$$f(\alpha,\beta,n)=\frac{1}{4\pi}$$
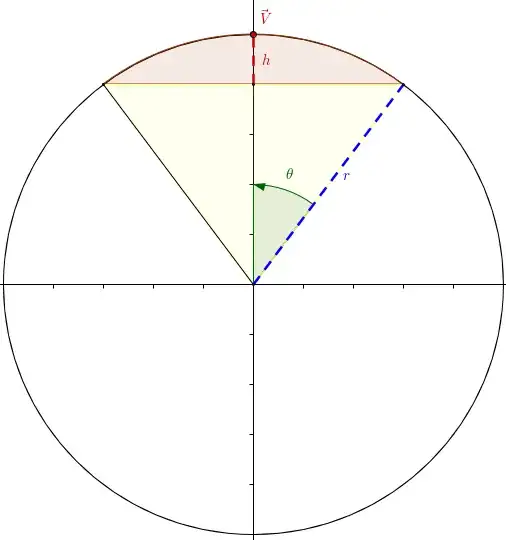
Another approach could be based upon the surface area of the cap of a central cone of a sphere.
The surface area of a spherical cap on a sphere of radius $r$ and associated with a central cone with aperture $2\theta$ is given by
$$ A=2\pi rh $$
where $h=r-r\cos\theta$ thus
\begin{eqnarray} A&=&2\pi r^2(1-\cos\theta\\ &=&4\pi r^2\left(\frac{1-\cos\theta}{2}\right)\\ &=&4\pi r^2\sin^2\left(\frac{\theta}{2}\right) \end{eqnarray}
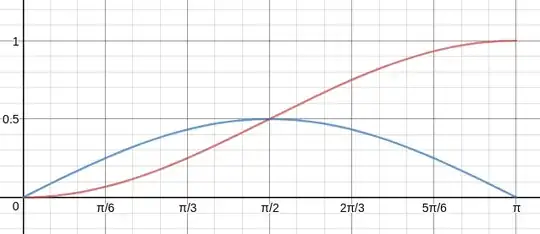
As a proportion of the entire surface area $4\pi r^2$ of the sphere we have the cumulative distribution function of the uniform distribution on the sphere
$$ F(\vec{V},\theta)=\sin^2\left(\frac{\theta}{2}\right) $$
and a probability density function of
$$ f(\vec{V},\theta)=\frac{1}{2}\sin\theta $$
You could also define it as $\frac{X}{||X||_2}$, where $X$ has multivariate normal distribution with zero mean and identity covariance matrix. Here it is shown, that this definition is equivalent to the aforementioned ones: Uniform distribution on the surface of unit sphere
