Given any three non-collinear points on a plane. Can there be an equilateral triangle such that the points lie on the perimeter of the equilateral triangle ?
Asked
Active
Viewed 392 times
2
-
I think at least one of the answers is worth accepting. It doesn't appear any others are forthcoming. – David K Jul 12 '17 at 04:58
3 Answers
2
Let $X$, $Y$ and $Z$ be our points.
Let $\hat{XY}=\hat{XZ}=240^{\circ}$ and let $C\in\smile{XY}$, $B\in\smile{XZ}$, such that $X\in BC$.
Now let $CY\cap BZ=\{A\}$.
Thus, since $\measuredangle XBZ=\measuredangle XCY=60^{\circ}$, we see that $\Delta ABC$ is an equilateral triangle.
Michael Rozenberg
- 203,855
1
Of course, just draw the line AB, draw a CX line at 60 degree from line AB, and finally close the triangle with a YZ line at 60 degree from both AB and CX.
Brethlosze
- 3,097
-
-
How do we prove that the given three points will lie on the perimeter of the equilateral triangle constructed? – Ananyo Bhattacharya Jun 06 '17 at 12:13
-
All lines are 60 degrees each other, and contain the points, so they lie on an equilateral triangle. – Brethlosze Jun 06 '17 at 12:15
1
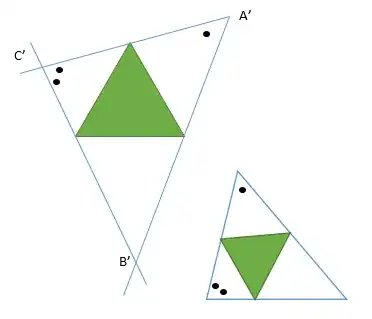
Think in reverse.
Take an arbitrary equilateral triangle.
From an outer point A', draw lines through two vertices, that form the same angle as CAB.
Then draw a third line that forms the angles ABC and BCA with the former, and translate it to the third vertex, giving the intersections B' and C'.
Now you have a triangle which is similar to the desired triangle and circumscribed to an equilateral triangle. Apply the similarity transform that maps A'B'C' to ABC, and you have it.
