Large powers of sine appear Gaussian -- why?

Question

As part of approximating an integral, I have noticed that $\sin^k(x), x\in[0, \pi]$ look almost identical to $\exp\left(-\frac{k}{2}(x-\frac{\pi}{2})^2\right)$ once $k$ is large enough (in practice, the two equations are visually identical for $k\geq 15$). As an example, see this picture of the two functions for $k=10$:

Can anybody explain why these functions practically are identical?

Edit: I should mention that the expression $\exp\left(-\frac{k}{2}(x-\frac{\pi}{2})^2\right)$ is derived by a 2nd order Taylor expansion of $\log\sin^k(x)$ around the mode $x_0 = \frac{\pi}{2}$, i.e. a Laplace approximation.

Answer 1

It's easier to shift $x$ by $\pi/2$ and establish the property for the cosine.

From Taylor and the limit definition of the exponential, for small $x$

$$\cos^kx\approx\left(1-\frac{x^2}2\right)^k=\left(1-\frac{kx^2}{2k}\right)^k\approx e^{-kx^2/2}.$$

The plot shows good convergence of $(1-t/k)^k$ to $e^{-t}$.

Answer 2

This is too long for a comment.

Semiclassical made a very good comment.

Let us use Taylor series around $x=\frac \pi 2$ $$\sin(x)=1-\frac{1}{2} \left(x-\frac{\pi }{2}\right)^2+\frac{1}{24} \left(x-\frac{\pi }{2}\right)^4+O\left(\left(x-\frac{\pi }{2}\right)^6\right)$$ $$\sin^k(x)=1-\frac{1}{2} k \left(x-\frac{\pi }{2}\right)^2+\frac{1}{24} k (3 k-2) \left(x-\frac{\pi }{2}\right)^4+O\left(\left(x-\frac{\pi }{2}\right)^6\right)$$ On the other hand $$e^{-\frac{1}{2} k \left(x-\frac{\pi }{2}\right)^2}=1-\frac{1}{2} k \left(x-\frac{\pi }{2}\right)^2+\frac{1}{8} k^2 \left(x-\frac{\pi }{2}\right)^4+O\left(\left(x-\frac{\pi }{2}\right)^6\right)$$ Computing the difference $$\sin^k(x)-e^{-\frac{1}{2} k \left(x-\frac{\pi }{2}\right)^2}=-\frac{1}{12} k \left(x-\frac{\pi }{2}\right)^4+O\left(\left(x-\frac{\pi }{2}\right)^6\right)$$ AT least, they are very close in the area around the maximum.

Answer 3

Another observation too long for a comment:

It's not actually that good of an approximation if you look at the ratio of $f_k(x) = \sin^k(x)$ to the value of the $g_k(x) = \exp ( - k (x- \pi/2)^2)$ for various values of $k$. Here are a few plots:

k = 1:

k = 5:

k = 25:

k = 125:

This trend seems to continue as $k$ increases.

Answer 4

Yet another observation too long for a comment:

Michael Seifert notes that the quality of match in the relative deviation of the two functions at hand worsens as $k$ is increased. However, the absolute deviation does improve with increasing $k$, as noted by OP.

Here MAD is the mean absolute deviation between the two functions, while MRAD is the mean relative absolute deviation, calculated at each point with reference to the value of the OP's Gaussian-type function. Both were calculated over the OP's $x\in [0,\pi]$ domain on a grid with spacing $\Delta x=\pi/100$.

So, the "quality of match" of the two functions with increasing k depends entirely on whether the relative or absolute deviation is most relevant to the application at hand.

Answer 5

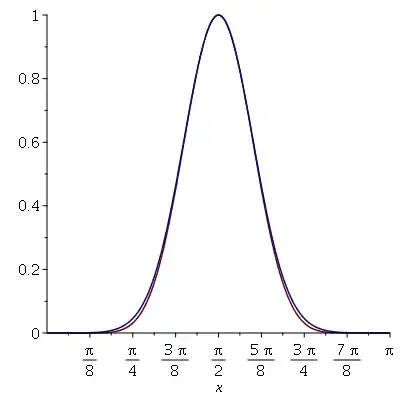
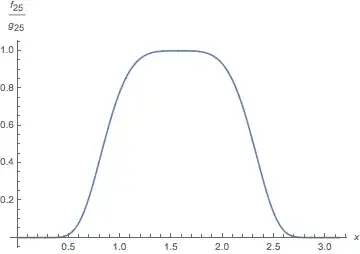
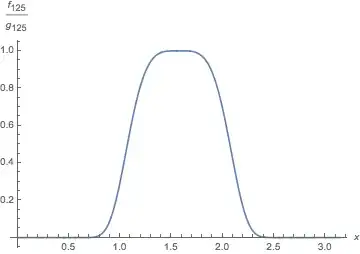
One thing that obscures the point in this exercise is that as $k$ increases, the Gaussian curve $y = \exp\left(-\frac k2(x-\frac\pi2)^2\right)$ develops a very narrow peak in the curve near $x=\frac\pi2$ surrounded by tails that are nearly zero. As long as the values of $\sin^x(x)$ are close enough to $\exp\left(-\frac k2(x-\frac\pi2)^2\right)$ near the very narrow top of the peak, the slope along the sides of the peak ($y$ values between $0.2$ and $0.9$ or other suitable bounds) becomes so steep that you could have a vertical error of several percent and the graphs would still appear very close because of the small horizontal distance to the nearest point on the other curve.

As it turns out, the approximation is really quite good, but it's hard to be sure just by looking at these graphs.

I think we get a better-controlled comparison when we compare all of the approximations to the same Gaussian.

To make things a little simpler, I suggest first shifting the graph left so that it is centered on the line $x=0$ instead of $x=\frac\pi2.$ After this shift, we would be comparing $\cos^x(x)$ with $\exp\left(-\frac k2 x^2\right).$

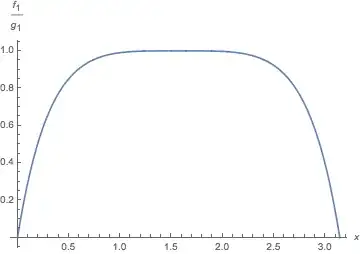
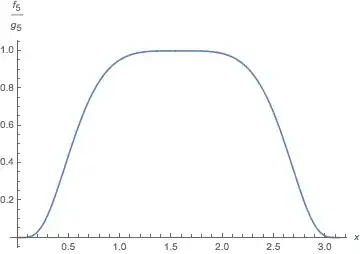
Next, we expand the graph in the horizontal direction by a factor of $\sqrt k.$ That is, we substitute $\frac x{\sqrt k}$ for $x.$ The Gaussian function then is $\exp\left(-\frac12 x^2\right).$ So we now will be comparing the sequence of sinusoidal functions $h_k(x) = \cos^k\left(\frac{x}{\sqrt k}\right)$ with the Gaussian $f(x) = \exp\left(-\frac12 x^2\right).$

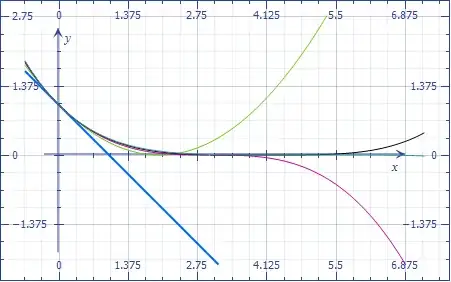
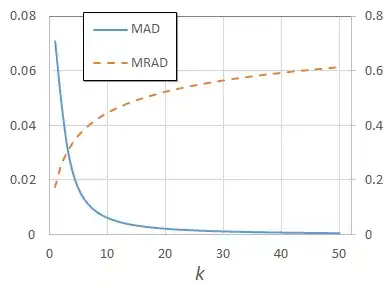
Plotting both $f$ and $h_k$ on the same graph, it is clear that $h_k$ approximates $f$ reasonably well over a wide interval for moderately large values of $k$. (For any particular $k,$ of course, $h_k$ will take the value $1$ at infinitely many values of $x,$ but as $k$ increases the gap between these values of $x$ increases.) Moreover, if we consider the relative error $\frac{h_k}{f} - 1,$ it is visually close to zero for $-\frac12 < x < \frac12$ even for $k=1,$ and the "flat" part of the curve $\frac{h_k}{f} - 1$ gets wider as $k$ increases.

For example, consider this Wofram Alpha graph. It shows that the error of $h_{100}$ relative to $f$ is less than half a percent when $-1.5 < x < 1.5.$

Taking a hint from Semiclassical and Claude Leibovici, let's consider the Taylor series of these functions. The Taylor series of $\exp\left(-\frac12 x^2\right)$ is $$ f(x) = 1 - \frac{x^2}{2} + \frac{x^4}{8} - \frac{x^6}{48} + \mathcal O(x^7). $$

The Taylor series of $\cos^k\left(\frac{x}{\sqrt k}\right)$ is $$ h_k(x) = 1 - \frac{x^2}{2} + \left(\frac18 - \frac{1}{12 k}\right) x^4 - \left(\frac1{48} - \frac1{24k} + \frac1{45k^2}\right) x^6 + \mathcal O(x^7). $$

It's clear that for any $x,$ at least the first two terms of the difference $$ f(x) - h_k(x) = \frac{1}{12 k} x^4 - \left(\frac1{24k} - \frac1{45k^2}\right) x^6 + \mathcal O(x^7) $$ disappear as $k \to\infty$; it seems that the other terms disappear as well.