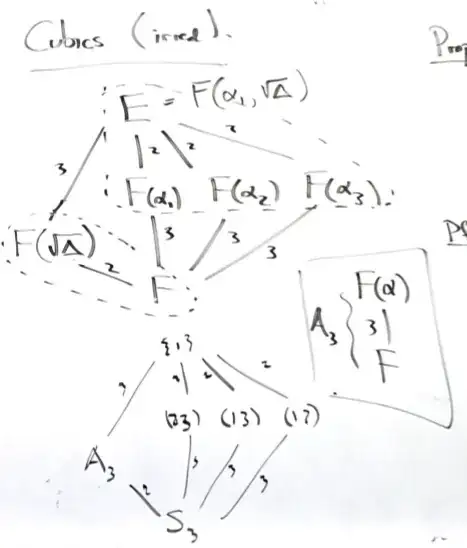
Let $f$ be an irreducible cubic polynomial with roots $\{\alpha_i\}$ and discriminant $D = \displaystyle \prod_{i \neq j} (\alpha_i - \alpha_j)^2$.
Claim: If $\sqrt{D} \in \mathbb{Q}$, then $\operatorname{Gal}(f) \cong A_3 \cong \mathbb{Z}_3$ and $\mathbb{Q}(\alpha_1)$ is the splitting field. Otherwise, if $\sqrt{D} \notin \mathbb{Q}$, then $\operatorname{Gal}(f) \cong S_3$ and we have a tower of proper inclusions $\mathbb{Q} \subset \mathbb{Q}(\alpha_1) \subset \mathbb{Q}(\alpha_1, \sqrt{D})$, with the latter the splitting field.
Proof: Suppose that $\sqrt{D} \in \mathbb{Q}$. Given that $\operatorname{Gal}(f)$ consists of all automorphisms of the splitting field of $f$ that also fix $\mathbb{Q}$, it must be the case that $\displaystyle \sqrt{D} = \prod_{i \neq j} (\alpha_i - \alpha_j)$ is fixed by all the elements of $\operatorname{Gal}(f)$. Each element of $\operatorname{Gal}(f)$ is determined by its action on the roots of $f$. Any permutation of the roots of $f$ that decomposes into an odd number of transpositions will change the sign of $\sqrt{D}$. Thus, $\operatorname{Gal}(f)$ can only contain even permutations, meaning it is a subgroup of $A_3$ (having at most $3$ elements). Since adjoining any root of $f$ to $\mathbb{Q}$ yields a degree-$3$ extension, it is forced that such an adjunction is the splitting field, and in fact $\operatorname{Gal}(f) \cong A_3$.
Now suppose $\sqrt{D} \notin \mathbb{Q}$. Since $D \in \mathbb{Q}$, it follows that $\mathbb{Q}(\sqrt{D})$ is a degree-$2$ extension of $\mathbb{Q}$. Consider the tower $\mathbb{Q} \subset \mathbb{Q}(\sqrt{D}) \subset \mathbb{Q}(\sqrt{D}, \alpha_1)$, where $\alpha_1$ is a root of $f$. We cannot have $\alpha_1 \in \mathbb{Q}(\sqrt{D})$ because $\alpha_1$ is an algebraic element of degree $3$. Therefore, $\mathbb{Q}(\sqrt{D}, \alpha_1)$ is an extension of $\mathbb{Q}$ of degree $6$. Since the Galois group of an irreducible polynomial is a subgroup of the permutation group on its roots, we must have $\operatorname{Gal}(f) \subseteq S_3$. This constricts the degree of the splitting field to a maximum of $6$, and from this we can see that $\mathbb{Q}(\sqrt{D}, \alpha_1)$ is the splitting field of $f$ with Galois group necessarily isomorphic to $S_3$.
Now, in general, if $\alpha_1$ is a root of a polynomial $f$ and $\deg(f) = n > 3$, then $\mathbb{Q}(\alpha_1, \sqrt{D})$, will not be the splitting field of $f$. In particular, this field has as degree at most $2n$, but all the symmetric groups $S_k$ appear as Galois groups of polynomials over $\mathbb{Q}$. If $\text{Gal}(f) \cong S_k$, its splitting field is of degree $k!$ over $\mathbb{Q}$. For a concrete example, any polynomial of prime degree $\geq 5$ with exactly $2$ complex roots has Galois group $S_p$.