Integral $\int_0^\infty \frac{dx}{x^a(1+x)}$ where $0

Question

I want to calculate integral $\int_0^\infty \frac{dx}{x^a(1+x)}$ where $0<a<1$. How can I do that? I need to use residue theorem or something like that?

Answer 1

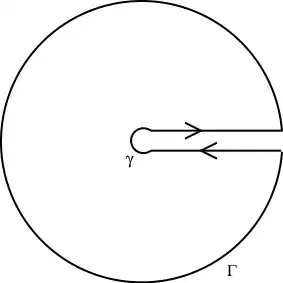
Yes, you'll need to use the residue theorem. Also note that since $a$ is not an integer, the integrand has a branch cut in the complex plane leading from 0 to ∞. The usual way to deal with this is with a "keyhole contour". There's a good example of this on Wikipedia, involving the integral of $\sqrt{x}/(x^2 + 6 x + 8)$ from 0 to ∞:

Normally the logarithm branch cut is defined as the negative real axis, however, this makes the calculation of the integral slightly more complicated, so we define it to be the positive real axis.

Then, we use the so-called keyhole contour, which consists of a small circle about the origin of radius $\epsilon$ say, extending to a line segment parallel and close to the positive real axis but not touching it, to an almost full circle, returning to a line segment parallel, close, and below the positive real axis in the negative sense, returning to the small circle in the middle.

Note that $z = −2$ and $z = −4$ are inside the big circle. These are the two remaining poles, derivable by factoring the denominator of the integrand. The branch point at $z = 0$ was avoided by detouring around the origin.

The techniques used for that example should also work for this one, with a bit of adaptation.

Answer 2

Notice how

\begin{align*} \int_0^\infty \frac{x^{s-1}}{1+x} \,\mathrm{d}x & = \int_0^\infty \int_0^\infty e^{-(1+x)y} x^{s-1} \,\mathrm{d}x \,\mathrm{d}y \\ & = \int_0^{\infty} \int_0^{\infty} e^{-y-u} \left(\frac{u}{y}\right)^{s-1} \frac{\,\mathrm{d}u}{y} \,\mathrm{d}y \\ & = \left( \int_0^\infty e^{-y} y^{-s}\,\mathrm{d}y\right)\left( \int_0^\infty e^{-u}u^{s-1}\,\mathrm{d}u\right) = \Gamma(s) \Gamma(1-s) \end{align*}

Since $\int_0^{\infty}e^{-(1+x)y}\,\mathrm{d}y = 1/(1+x)$ and the second equality follows from the substitution $x \mapsto u/y$. The last expression is simply the Euler reflection formula

$$ \Gamma(s) \Gamma(1-s) = \frac{\pi}{\sin \pi s} $$

While the formula above often is shown using complex analysis it may also be done by using the Weierstrass-product for sine.

---

For a step by step solution for evaluating the integral using complex means, you can look at my answer here complex analysis definite integral. While I do solve a bit more general integral, the steps are the same. There are also other answers evaluating the integral in a number of different ways.