1

Trying to mimic the procedure in this answer on a slightly more difficult problem: How to calculate the trajectory of a point on a cork screw.

I have built a matrix that can calculate it for me

$${\bf M}(\delta) = \left({\bf I}+\left[\begin{array}{cc}{\bf R}(\delta)&0\\0&{\bf S}(\delta)\end{array}\right]\right)^{}$$

With $${\bf R}(\delta)=\left[\begin{array}{cc}0&-\delta\\\delta&0\end{array}\right]$$

Being the principal matrix logarithm of the rotational group (as explained in the answer I linked to). And:

$${\bf S}(\delta)=\left[\begin{array}{cc}0&\delta\\0&0\end{array}\right]$$

If I do this, then just as claimed in answer I can verify that ${\bf M}(\delta)^{1/\delta}[v_x,v_y,0,1]^T$ does rotate one radian of $x$ and $y$ and simultaneously move 1 unit in the screwing dimension (third position in the vector: $z$).

But I am unsure how to motivate what $\bf S$ looks like. Obviously the derivative should be $1$ everywhere since the derivative of $f(t) = t$ which I want the screwing to follow (constant "speed" in z-direction) is 1 everywhere. But why does it end up in the upper right corner?

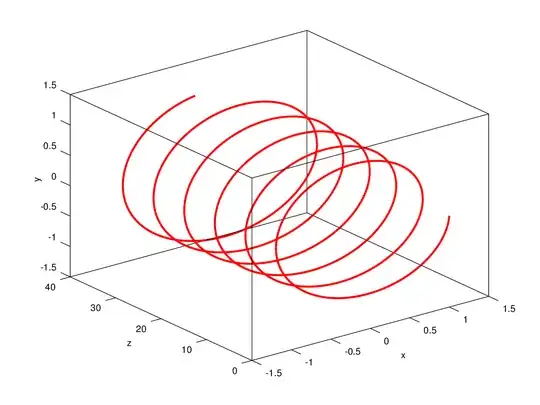
Here is the screwing motion I want to represent, constant angular speed and constant "forward" motion (in z dimension): enter image description here

mathreadler
  • 26,534

1 Answers1

1

Not a matrix solution but for "corkscrew" motion along initial point $\vec x$ and direction $\hat u$ you can do this

$$\vec x + \hat ut + \hat v\cos(t) + \hat w \sin(t)$$ where $$\hat v = \frac{\vec x - P_{\hat u}(\vec x)}{||\vec x - P_{\hat u}(\vec x)||}$$ $$\hat w = \hat v \times \hat u$$ $P$ stands for orthogonal projection

user447223
  • 26
  • The purpose of the question was to use the relatively simple corkscrew motion as a step in learning the techniques to systematically build matrix representations for more complicated things where other ways would be more complicated, but thank you anyway. – mathreadler May 17 '17 at 13:32