Tangent of a circle through a point not on circle

Question

Given the equation of a circle: $(x+4)^2+(y-2)^2 = 1$ find the tangent that goes through the point $(-3,3)$…

…but this point IS NOT on this circle. Unfortunately, this is not something that I have seen before and the normal formula doesn't work.

Thank you

There are exactly two such tangents. As a hint, recall that the lines are perpendicular if and only if the products of their slopes is $-1$. — Mathematician 42, May 08 '17 at 13:25
@Mathematician42 But the given point is in the circle. Thus there are no tangents at all. — Parcly Taxel, May 08 '17 at 13:26
@ParclyTaxel: Holy cow, you're right, the point is in the circle! Then this question makes no sense. There must be an error in the exercise. — Mathematician 42, May 08 '17 at 13:27
See also this famous ill-posed question from Vladimir Arnold. — Parcly Taxel, May 08 '17 at 13:28
One way to show (-3,3) is in the circle is to plug the coordinates in. Since the point (1 000 000, 1 000 000) has a value greater than 0, points inside the circle have values less than 0. Since the value of the expression with (-3,3) is -9, the point is therefore inside the circle. — Toby Mak, May 08 '17 at 13:30
@ParclyTaxel: He would have fooled me I guess, it's a fun fact though. — Mathematician 42, May 08 '17 at 13:32
@ParclyTaxel OH NO! this is a little embarrasing, but i made a typo. its supposed to be 1 not 11 (my keyboard is terrible). I'm very sorry and i will try my best to proof read my work better! — John Hon, May 09 '17 at 12:04
@ParclyTaxel yes i doubled checked, a tangent through (-3,3) — John Hon, May 09 '17 at 12:10

score 2 · Accepted Answer · answered May 09 '17 at 12:11

2

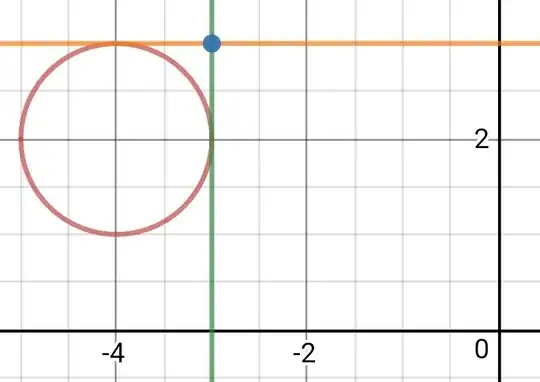A little graphing won't hurt: By inspection, the tangent lines are $x=-3$ and $y=3$.

answered May 09 '17 at 12:11

Parcly Taxel

105,904

yeah this is what i gathered from my teacher. However is this the only way? what if the line was not vertical or horizontal though? – John Hon May 09 '17 at 13:39
@JohnHon The idea when finding a tangent generally is to consider the right-angled triangle between the circle centre, the point in question and the point of tangency. A little wringing of algebra then obtains the tangent lines; I suggest you search Stack Exchange (yes, this site) for more information. – Parcly Taxel May 09 '17 at 13:45

score 0 · Answer 2 · answered May 08 '17 at 13:46

0

Well there's a formula you could use:

$$(y-b)=m(x-a)\pm r\sqrt{1+m^2}$$

for a circle $(x-a)^2+(y-b)^2=r^2$

Although (3,3) ain't giving you a tangent

answered May 08 '17 at 13:46

The Dead Legend

4,837

score -1 · Answer 3 · answered May 08 '17 at 13:29

-1

You should have a system of equation the first is the circle and the second is the general equation for a line that pass from $(3,3)$ substitute one into the others and apply the tangent condition $b^2-4ac=0$ you will find the two points. Another methods is using the derivation.

answered May 08 '17 at 13:29

user154508

39
1
4

The point $(-3,3)$ is inside the circle so there are no tangents which pass through this point - this method will give erroneous solutions – lioness99a May 08 '17 at 13:45
It will give a non real solution – user154508 May 08 '17 at 13:53

Tangent of a circle through a point not on circle

3 Answers3