In the definition of limit why delta depends on epsilon ? why not epsilon depends on delta?

Question

Please anyone help me i am bothered with epsilon I delta definition of limit. Can anyone had a good explanation of epsilon I delta definition.

Answer 1

A somewhat different take on the question than the others:

You can define anything you want, so let's try it. (I'll work in $\Bbb R$; if you know how to define limits in other contexts then you know enough to do the translation.)

We say that $K$ is a kimit of a function $f$ at $x=a$, if for all (positive) $\delta$ there exists a (positive) $\varepsilon$ such that for all $x$ such that $|x-a|<\delta$, we have $|f(x)-K|<\varepsilon$.

Because of the order of quantifiers (that the other answers explain well), in this definition we have that $\varepsilon$ depends on $\delta$ (it might not for any particular example, but it could, in general).

Let's try to calculate some kimits.

Consider the constant function $f(x)=1$. It's reasonable to suspect that $K=1$ is a kimit of $f$ at $x=0$. So let's try:

• Obviously $|f(x)-K|=1-1=0$, and this is true no matter what $x$ is. So, for any $\delta$ we can choose $\varepsilon=0.7385$, and then it's certainly true that if $x$ is within $\delta$ from $0$ (i.e. if $|x-a|<\delta$), then $f(x)$ is within $0.7385$ from $1$ (i.e. $|f(x)-1|<\varepsilon$).

So the definition is satisfied, and $1$ is a kimit of $f$ at $x=0$.

However, we don't, a priori, have any guarantee that kimits are unique. So just for fun, let's try $K=2$.

• Obviously $|f(x)-K|=|1-2|=1$, and this is true no matter what $x$ is. So let's choose $\varepsilon=1+\delta$. It's certainly true that if $x$ is within $\delta$ of $0$, then $|f(x)-K|<1+\delta$.

So the definition is still satisfied. That is, $2$ is also a kimit of $f$ at $x=0$

If you meditate on the way we made these arguments, you will realize that in fact any number $K$ is a kimit of this $f$ at $x=0$.

---

Again, you can define whatever you want, so we could keep playing with kimits and see what happens. But if you're trying to think about the idea of 'where the function is going toward near $x=a$', then this example shows us that kimits are a terribly bad way of capturing this idea.

Answer 2

The informal definition of $\lim_{x\rightarrow a} f(x) = c$ is

$f(x)$ can be be made arbitrarily close to $c$ by making $x$ close to $a$.

This captures the idea that $f(x)$ should not jump suddenly away from $c$ when $x$ moves away from $a$. Instead, the process is gradual in the sense that no matter how close you want $f(x)$ to be to $c$, you can achieve this by making $x$ close to $a$.

Imagine two people taking a close look at the curve $y = f(x) = x^2$.

Mathematician: So as you can see, the curve is perfectly smooth near $x=2$. That is, there's no sudden leap away from $f(2) = 4$ when $x$ moves away from $2$. Thus...

Skeptic: I don't see any reason to believe this.

Mathematician: It's perfectly clear. See? (Points to the parabola.) Nice and smooth.

Skeptic: You are naïve. It only looks smooth from far away. If you zoom in to a smaller scale you'll surely see the jump. I'm sure if you set $\epsilon = .1$ you'll be able to see this jump - surely there's no $x$ close enough to $2$ so that $f(x)$ is that close to $4$.

Mathematician: (sigh) Fine. If you insist we can look closer. (takes out magnifying glass) if we look on the smaller scale, we see that if $x$ is within $\delta = .024$ of $2$ then $f(x)$ is within $.1$ of $4$.

Skeptic: Fine. But again, we're just seeing the macroscopic picture. I'm sure if you zoom in you'll see the discontinuity here. Just try to get $f(x)$ within $\epsilon = .0001$ of $4$.

Mathematician: (exasperated) Fine. (Takes out microscope...)

etc. For each $\epsilon$, we let the mathematician pick a new $\delta$. This seems only fair, and intuitively captures the notion of continuity.

Answer 3

Because quantifiers don't commute per say.

First you should state the def!

limit def $$\lim_{x \to a}f(x)=L$$

If $\forall \epsilon \gt 0 \ ,\exists \delta \gt 0 \ ( |x-a|\lt \delta \Rightarrow |f(x)-L| \lt \epsilon)$

NOT limit def $$\lim_{x \to a}f(x)=L$$

If $\forall \delta \gt 0 \ ,\exists \epsilon \gt 0 \ ( |x-a|\lt \delta \Rightarrow |f(x)-L| \lt \epsilon)$

And NOT

$$\lim_{x \to a}f(x)=L$$

If $\exists \delta \gt 0 \ ,\forall \epsilon \gt 0 \ ( |x-a|\lt \delta \Rightarrow |f(x)-L| \lt \epsilon)$

Universal and existential quantifiers do not commute. And they do not mean the same thing. They aren't tautologies or equivalent statements. One is defined as the definition of the limit and one isn't.

Answer 4

Perhaps using examples is a way to describe the idea, consider$$ f:[0,\infty)\rightarrow [0,\infty) $$ defined by $$f(x)=x^2$$ Then we plot the graph of it, (sometimes mathematics comes from intuition) the graph should be continuous. So intuitively, we want a limit such that $\lim_{x\rightarrow x_0}=f(x_0), \forall x_0\in [0,\infty)$.

Continuity should follows from the limit process by talking about the neighborhood of a particular point. If the limit process gives the same value of the function value at that point, then we would like to say it is continuous. So the definition should be natural (provided we have the limit).

So we need to discuss whether the limit process satisfies our intuition. If we let $\delta$ go first, then what we get is: $\exists \delta>0$ such that $\forall \epsilon>0$, we have $|f(x_0)-f(x)|<\epsilon$ whenever $|x-x_0|<\delta$. So $f$ would not satisfy the condition when $x_0$ is large enough. But the other way round solves this problem perfectly.

Answer 5

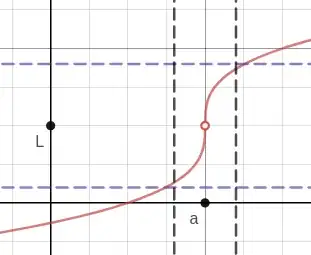
Perhaps it would help to think of it geometrically using a diagram. We want to understand the meaning the $\epsilon,\,\delta$ definition of limit.

$$ \lim_{x\to a}f(x)=L $$

Geometrically this equation means that if we pick any positive number $\epsilon$ and then select two horizontal lines lying a distance $\epsilon$ above and below the line $y=L$, that is, the two horizontal dashed lines pictured below

1. $y=L+\epsilon$

2. $y=L-\epsilon$

then we will always be able to find a positive number $\delta$ so that there are two vertical lines

1. $x=a+\delta$

2. $x=a-\delta$

such that any point of $f$ between the vertical lines must also lie between the horizontal lines.

The important thing to notice is that if one makes $\epsilon$ smaller, it may be necessary to make $\delta$ smaller as well. Otherwise there may be points of $f$ lying between the vertical lines but not lying between the horizontal lines.

So the choice of $\delta$ may have to adjust to any change in $\epsilon$. That is, the choice of the value of $\delta$ depends upon the choice of $\epsilon$.