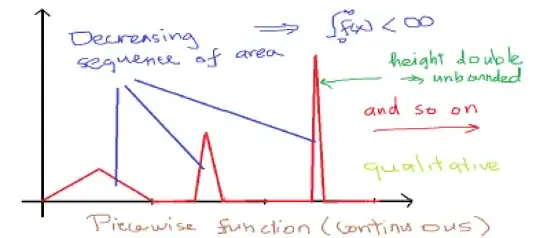
Let $h:[1, \infty)\rightarrow \mathbb R$ a continuous non-negative function, such that $\int_{1}^{\infty} h(x)\ dx$ converges. does $h$ must be bounded in $[1, \infty)$?
I tried to prove it by showing that if $\int_{1}^{\infty} h(x)\ dx$ converges, then by the definition the $\lim_{b \to \infty}\int_{1}^{b} h(x)\ dx$ exists. Can I conclude that from the existence of this limit, the function $h$ is bounded?
This statement is false. Consider a function $f$ which is usually $0$, except for a triangular "bump" that happens at each natural number. The bump has width $1/n^3$ and height $n$, and so it has area $\frac{1}{2n^2}$. Then we have $$\int_1^\infty f(x) dx = \sum_1^\infty \frac{1}{2n^2} = \pi^2/12 < \infty$$ But $f$ is not bounded, since the bumps get arbitrarily large.
More formally, if $x$ is a real number greater than or equal to $1$ then we may uniquely express $x$ in the form of $x=n+\varepsilon$, where $n\in \mathbb{N}$ and $\varepsilon \in [0,1)$. Then let $f(x) = 0$ if $\varepsilon > 1/n^3$, $f(x) = (2/n^2)(x-n)$ if $\varepsilon < 1/(2n^3)$, and $f(x) = -(2/n^2)(x-n-1/(2n^3))$ otherwise.
Simple answer: no. $$ f(x)=\sum_{n\geq 1}n\,e^{-n^6(x-n)^2} $$ is a continuous, positive and integrable function on $\mathbb{R}^+$, but it is unbounded since $f(n)\geq n$.
