The following question came to me as I was reading about local connectedness:
Let $$S := \{x \in X \mid X \text{ is locally connected at } x \},$$ where $X$ is some topological space. Is $S$ generally open in $X$? If not, suppose it is. Would this tell us much about the space $X$?
Here is the definition of local connectedness I am working with:
A space $X$ is said to be locally connected at $x$ if for every neighborhood $U$ of $x$, there is a connected neighborhood $V$ of $x$ contained in $U$.
Let
$$X = \{0\} \times\mathbb{R} \cup \bigcup_{n = 1}^{\infty} \{ (x,y) : (x-n)^2 + y^2 = n^2\},$$
in the subspace topology induced by $\mathbb{R}^2$.
Then $X$ is locally connected at $(0,0)$ - every $B_r((0,0)) \cap X$ for $r > 0$ is connected - but $X$ is not locally connected at any $(0,y)$ with $y \neq 0$, so $S$ is not open.
Generally, $S$ being open alone doesn't tell us much about $X$. $S$ is of course locally connected then, and the exterior of $S$ is nowhere locally connected, but both of these can happen in many ways.
Would this tell us much about the space $X$?
It can tell us something about nice embeddings of $S$, and by extension, something about $X$.
If $X$ is compact and $S$ is open, then shrinking $X\setminus S$ to a single point $\infty$ produces a compact locally connected space $S\cup \{\infty\}$. In particular, $X$ maps onto a locally connected space via a continuous extension of the identity on $S$.
This is a very nice result if you are interested in compactifications.
Theorem 4.1 in this paper also says that $X$ is locally connected if $\overline S=X$ and $X\setminus S$ is totally disconnected. For instance, consider $X=[0,1]$, $S=(0,1)$, and $X\setminus S=\{0,1\}$. Compare to the topologists sine curve.
There are basically no 'general results' about this set, even in very nice settings.
'Locally Connected': X has an open neighborhood base of connected sets at $x$.
'Connected im Kleinen': X has a neighborhood base of connected sets at $x$.
So, your definition is what is usually called cik (though sometimes, the former is called 'strongly locally connected' and your definition is 'locally connected'). The latter is strictly weaker than the former, even in the case of continua (compact, connected metric spaces). Even in the case of simply connected $1$-dimensional planar continua. Check the right end-point here.
This set is not necessarily open, but it can be. This set is not necessarily closed, but it can be. This space can have finitely many, countably infinitely many or uncountably many components. It may or may not separate $X$. It's easier to look at its complement, $N(X) = \lbrace x \in X : X$ is not cik at $x \rbrace$.
In the topologist's sine curve, $N(X)$ is closed, and both it and its complement have one component. In the two-sided topologist's sine curve, $N(X)$ does separate $X$. If you 'chain' an infinite sequence of topologist's sine curves so they converge to a point, then everything gets separated and $N(X)$ is not closed, since the 'end point' will be cik (even lc). In that case, both $N(X)$ and its complement have countably infinitely many components, though.
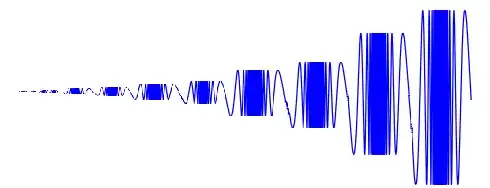
$N(X)$ in the Cantor Comb has uncountably many components. To get uncountably infinitely many components in $S$, attach a Cantor Fan to the point $(0,1)$ on the topologist's sine curve.
