Two tangents are drawn from a point $P$ to the circle $x^2+y^2=1$. If the tangents make an intercept of $2$ on the line $x-1=0$, then what is the locus of $P$?
A) Parabola
B) Pair Of lines
C) Circle
D) Straight Line
What i did was to assume two tangents from point $P$ as $$y=mx \pm \sqrt{m^2+1}$$
and equate it with $x=1$. Sure it gives a value but how do i decide the ordinate then? Should I use symmetry or there is a better sophisticated method for this one?
This is not a solution. The following figure is just my guess on the meaning of the question.
Let $A$ and $B$ be points on $x=1$ such that $|\overline{AB}| = 2$. With $R$ the point where $x=1$ meets the circle, define $\alpha := \angle ROA$ and $\beta := \angle ROB$. Let the "other" tangent from $A$ meet the circle at $S$; we see that $\angle ROS = 2\alpha$. Likewise, the "other" tangent from $B$ meets the circle at $T$ such that $\angle ROT = 2\beta$. Let these "other" tangents intersect at $P$, and note that $\overline{OP}$ bisects $\angle SOT$. Consequently, we can write $$\begin{align} P &= \sec(\alpha-\beta)\;\left( \cos(\alpha+\beta), \sin(\alpha+\beta) \right) \\ &= \left( \frac{\cos\alpha \cos\beta - \sin\alpha\sin\beta}{\cos\alpha\cos\beta + \sin\alpha \sin\beta}, \frac{\sin\alpha \cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta + \sin\alpha \sin\beta} \right) \\ &=\left( \frac{1 - \tan\alpha\tan\beta}{1 + \tan\alpha \tan\beta}, \frac{\tan\alpha+\tan\beta}{1 + \tan\alpha \tan\beta} \right) \end{align}$$
We can get the equation for the locus by eliminating $a := \tan\alpha$ and $b := \tan\beta$ from the system $$x = \frac{1-a b}{1+ab} \qquad y = \frac{a+b}{1+ab}$$ subject to the "intercept condition" $$a - b = 2$$
Without too much trouble, we arrive at the relation
$$ 2( 1 + x ) = y^2$$
which describes a parabola. $\square$
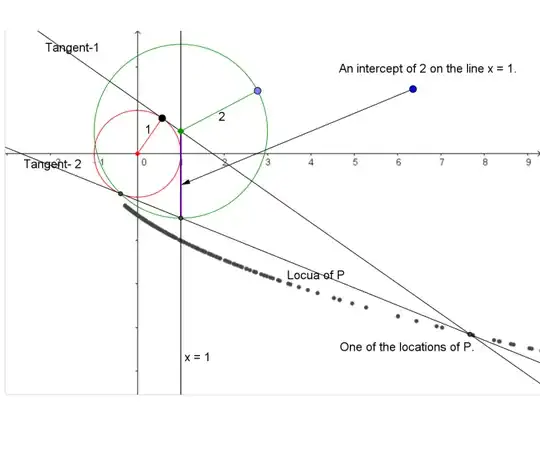
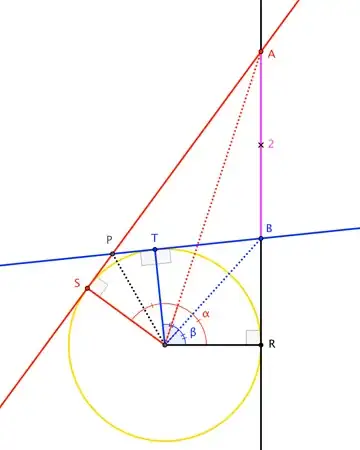
It is somewhat of a well known result that the equation of a pair of tangents to conic $S$ from a point $P(h, k)$ is obtainable using $S(h,k)S(x,y)=T(x,y)^2$. A proof for this might be found in the answers to this query on this site.
Obtain the equation for pair of tangents in this case as: $$(x^2+y^2-1)(h^2+k^2-1) = (hx+ky-1)^2$$
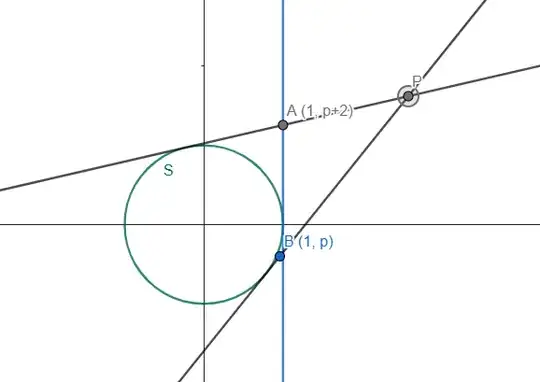
This is satisfied by the points $A(1, p +2)$ and $B(1, p)$, for some $p$, lying on $x=1$ to conform to the given restrictions. Hence,
$$p^2(h^2+k^2-1) = (hx+kp-1)^2$$ $$(p+2)^2(h^2+k^2-1) = (hx+k(p+2)-1)^2$$
Once may eliminate $p$ from the above to equations to obtain a relation between $h$, and $k$. This comes out to be: $$h = \frac{1}{2}(k^2-2)$$
Rearranging, and replacing $h$ with $x$ and $k$ with $y$, we obtain the equation for a parabolic locus for $P$: $$y^2 = 2(x+2)$$
Comment: It is possible to obtain an answer without involving any of this by an analysis of the options themselves. This is by no means rigorous, or educative, but such heuristics are nonetheless pleasant. It is easy to establish that whatever the locus may come out to be, it must be symmetric about the x-axis. No single line symmetric about the x axis seems to satisfy our conditions. A pair of lines may also be eliminated with a bit of sketching. Curiously enough, a point at inifinity, subtending parallel tangents satisfies our criteria. This rules out the circle, and leads us to the parabola.
