I have a simplified version of the wave equation which I need to solve using variable separation. This formulation is destined to represent the propagation of a wave in a thin column subjected to a constant load on the free end and fixed at the bottom end ("standing wave"):
GOVERNING PDE
$$u_{xx} = u_{tt}$$
Since this is not a "book problem" the boundary/initial conditions are a bit fuzzy to me. I am however quite certain of the following:
BOUNDARY CONDITIONS $$u(0,t) = 0 $$ $$u_x(L,t) = 1$$ $$u_t(0,t) = 0$$
First arises from fixed end, second from constant load and 3 again from fixed end.
INITIAL CONDITIONS $$u(x,0) = 0$$ $$u_t(x,0) = 0$$
Represents the at-rest state of the column before loading is applied.
ATTEMPTED SOLUTION
I tried to solve this equation by variable separation but reached a dead end:
The separation of variables assumption states that $u(x,t) = X(x)T(t)$ which breaks the problem down into a set of two ODE's as follows:
$$X''+\omega^2X=0$$ and, $$T''+\omega^2T = 0$$
For which the solutions are $$X(x) = A\sin\omega x+B\cos \omega x$$ and $$T(t) = C \sin\omega t+D\cos \omega t$$
Applying BC (1) yields $B=0$. IC (1) yields $D=0$ then we are left with:
$$AC\omega \cos (\omega L) \sin (\omega t)=1$$ and $$AC \sin (\omega x)=0$$
Which is sort of a dead end... since we cannot solve for constant $AC$. Does anyone know how to approach this specific problem using separation of variables?
EDIT
After following though with @DisintegratingByParts solution, I got the following results:
$$B_n = \frac {-2L}{(n+\frac{1}{2})^2\pi^2} \sin \left(\left(n+\frac{1}{2}\right)\pi \right)$$
Therefore
$$u(x,t) = v(x,t)+x$$ and $$v(x,t) = \sum_{n=0}^{\infty}B_n\sin((n+1/2)\pi x/L)\cos((n+1/2)\pi t/L)$$.
Because
$$u(x,t) = v(x,t)+x$$ and $$v(x,t) = \sum_{n=0}^{\infty}\frac {-2L}{(n+\frac{1}{2})^2\pi^2} \sin ((n+1/2)\pi)\sin((n+1/2)\pi x/L)\cos((n+1/2)\pi t/L)$$,
$$u(x,t) = x+\sum_{n=0}^{\infty}\frac {-2L}{(n+\frac{1}{2})^2\pi^2} \sin ((n+1/2)\pi)\sin((n+1/2)\pi x/L)\cos((n+1/2)\pi t/L)$$
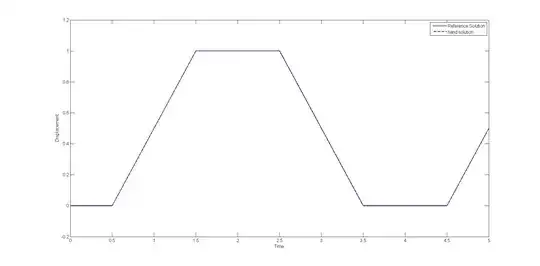
Plotting this for $x=L/2$ and $t$ from $0$ to $5$ against a reference solution yields the following plot
Where the red is the reference solution and the blue is the solution proposed by @DisintegrationByParts.
EDIT 2
The reference solution I am using is the following: 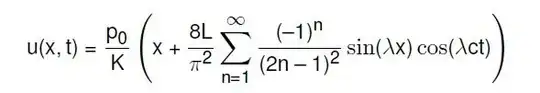
where $\lambda = \frac {(2n-1)\pi}{2L}$ and $p_0=K=L=c=1$