Infinite Series for Log(x)?

Question

Is there any series for natural log(x) where x is any number,unlike Taylor series for log(1+x) where |x|<1?

Answer 1

There can't be a standard power series because the logarithm is singular at $x=0$.

Anyway, one can consider the Taylor expansion of

$$\log\frac{1+t}{1-t}=\log(1+t)-\log(1-t)=2\sum_{k=0}^\infty\frac{t^{2k+1}}{2k+1}$$ which is convergent for $|t|<1$.

Then

$$x=\frac{1+t}{1-t}\iff t=\frac{x-1}{x+1}$$ and this transformation maps the positive $x$ to the convergence interval.

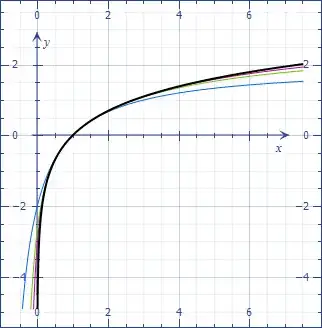
On the plot, the first three approximations and the exact function (in black).

Answer 2

I assume you mean $x \in \mathbb{C}$. First, observe that the series expansion $$\ln(r)=2\sum_{n=0}^\infty\frac{1}{2n+1}\left(\frac{r-1}{r+1}\right)^{2n+1} $$ produces the familiar logarithm for any $r>0$. For the general case write $x=r \exp{i \theta}$ with $r=|x|,\theta=\arg{x}$, and you'll find that $$\log(x)=\ln r+i \theta=\ln|x|+i \arg{x}$$ where you can expand the $\ln|x|$ term as above. However, since the argument of a nonzero complex number is multi-valued, you will encounter problems when trying to expand the other term.