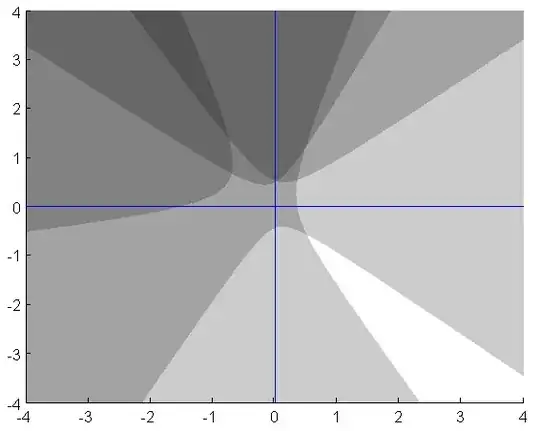
Let us formalize your question. (see first picture below)
Let $A_{0,a,b}$ be the region defined by inequality
$$\tag{*}\frac{x^2}{a^2}-\frac{y^2}{b^2}>1,$$
and $A_{\theta,a,b}$ the image by a rotation of angle $\theta$ of region $A_{0,a,b}$ (this rotation having its center in 0).
The essential property is that all regions $A_{\theta,a,b}$ are convex.
As the intersection of any number of convex sets is convex (Proof that the intersection of any finite number of convex sets is a convex set), you have a convex result (the darker region in the picture).
Last topological point: a convex set is a connected set (Show that any convex subset of $R^k$ is connected) i.e. is a "whole", in the sense that it cannot be in two or more separate parts.
Now, after an explanation with WYC (see our exchanges), one can consider the case I have treated upwards as exceptional. The general case where complementary regions: $B_{0,a,b}$ defined by inequality
$$\frac{x^2}{a^2}-\frac{y^2}{b^2}\leq1$$
are used as well, with $B_{\theta,a,b}$ defined in the same way as $A_{\theta,a,b}$ in (*). Note that $B_{\theta,a,b}$ is a concave set.
Thus the true question is as follows: Let $C_{\theta,a,b}$ equal either to a $A_{\theta,a,b}$ or to a $B_{\theta,a,b}$.
What can be said of a finite intersection :
$$C_{\theta_1,a_1,b_1} \cap C_{\theta_2,a_2,b_2} \cap \cdots \cap C_{\theta_n,a_n,b_n} ?$$
In particular, is it a connected set ?
The Matlab program given below provides a visual picture (see Fig. 2) of this intersection.
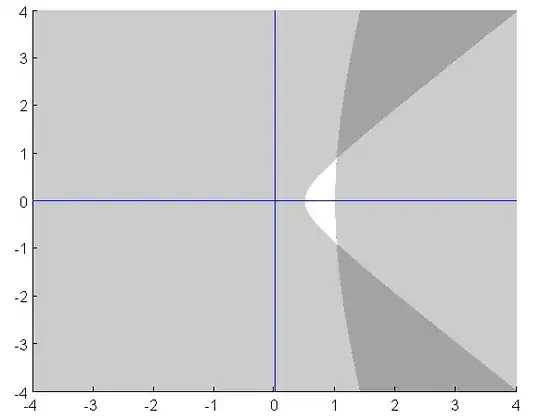
But the answer to the connectedness is no in general. It suffices (see fig. 3) to consider branches of hyperbolas $H_1$ and $H_2$ with resp. equations $y=\pm \sqrt{x^2-0.25}$ and $y=\pm \sqrt{x^2-1},$ and take the convex region to the right of $H_1$ and the concave region to the left of $H_2$.
Matlab code that has generated the second figure:
clear all;close all;hold on;
L=4;axis([-2,L,-2,L]);
set(gcf,'color','w');
plot([-L,L],[0,0]);plot([0,0],[-L,L]);
t=-5:0.01:5;
% 3 convex regions:
for k=1:3
f=cosh(t)/(1+2*rand)+i*sinh(t)/(1+2*rand);
s=rand;ro=exp(i*(pi)*s);
f=ro*exp(i*(pi/2)*rand)*f;
g=fill(real(f),imag(f),'k');
set(g,'EdgeAlpha',0)
alpha(0.2);
end;
% 2 non convex regions (complementary set of convex regions):
for k=1:2
f=cosh(t)/(1+2*rand)+i*sinh(t)/(1+2*rand);
f1=[f,-f];
r=rand;
s=rand;ro=exp(i*(pi)*s);
f=ro*exp(i*(pi/2)*r)*f;
g=fill(real(f),imag(f),'k');
set(g,'EdgeAlpha',0)
alpha(0.2);
f1=ro*exp(i*(pi/2)*r)*f1;
g1=fill(real(f1),imag(f1),'k');
set(g1,'EdgeAlpha',0)
alpha(0.2);
end;