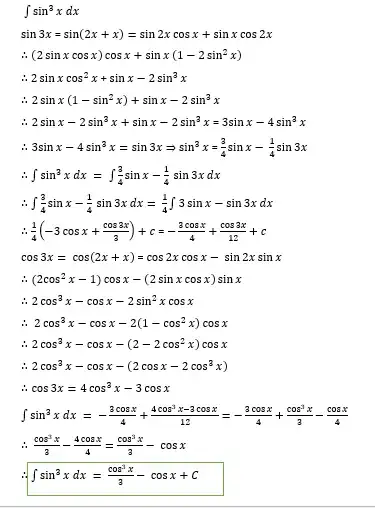What is this constant 'C' in integration? Why is it different when I integrate using different techniques?

Question

Method 1:

Method 2:

In these two images, you will see that I have integrated $\sin^3 x$ using different techniques. As you can see I get different answers. I asked my teacher why this is and he said it is because the constants '$C$' are different for each one.

Can someone please explain to me what that means? Also, Why does it vanish when we add limits?

I know this is a relatively easy question for this site, but could you be wary I am only 16. So, could you make your answers simple enough for me to understand?

Secondly, you'd've seen that I showed my working out in the images. I did this using word - WHICH TOOK A LIFETIME! Do you have any suggestions of apps, websites or literally anything that could speed up digitalising my working out for maths?

Thanks, IB

Answer 1

Your teacher was referring to a true fact that is worthwhile for you to know, although as it turns out, it does not apply to your two calculations.

To understand what your teacher is talking about, we need to remember that $\int f(x)\,dx$ does not describe a single function, but rather a family of functions containing every function whose derivative is $f.$ Each member of that family of functions is an antiderivative or primitive of $f.$

Since the notation for a family of functions like this is a bit complicated, we usually indicate the solution of an indefinite integral by writing down just one of its antiderivatives, that is, one representative from the family of functions that solves the integral. The $+C$ term is an acknowledgement that the choice of which function to write is arbitrary; it says that in order to say which of the antiderivatives of $f$ we have written, we just have to choose a value for the constant $C.$ A different choice will give us a different antiderivative, but it belongs to the same family of functions.

It often happens that when you use two different methods to integrate a function, you end up with answers that look different, in much the same way that your two answers look different. In those cases, your teacher is correct: if you remove the $+C$ from each answer, the functions that remain differ by a constant amount, and that is the difference your teacher referred to. An example of this is in this answer to another integration question

In a definite integral of $f,$ again we can use any antiderivative of $f$ in the solution, but we must use the same antiderivative at both ends of the interval of integration. So whatever the amount is by which the antiderivative you chose is greater than the antiderivative someone else chose, the difference cancels out when you subtract the value at one end from the value at the other.

In your particular integral, however, in your first attempt at the solution you simplified $[1 - (2\cos^2 x - 1)]$ to $-2\cos^2 x.$ That is incorrect. In fact, $$[1 - (2\cos^2 x - 1)] = 2 - 2\cos^2 x.$$ The missing term $2$ is why you are missing the term $-\cos x$ at the end. That is, your first result is simply wrong, not just using a "different constant $C$" than your second result.

Answer 2

$\int f(x) dx$ is a function, $F(x)$ so that $F'(x) = f(x)$. If $F(x)$ is such a function, then if $G(x) = F(x) +k$ for some constant $k$ then $G'(x) = F'(x)$ and ... well, then $\int f(x) dx$ could logically just as likely be $G(x)$ as well as $F(x)$ and there is no way to say one is correct and the other is wrong. So $\int f(x) dx $ is not one function but an infinite set of functions. But what all these functions have in common is that they all equal one another plus or minus some constant value difference between them.

In other words if $H'(x) = J'(x)= h(x)$ then $H(x)=J(x) + C$ for some $C$ and we say $\int h(x) dx = H(x)$ or any other $J(x) = H(x) + C$ for some constant.

or $\int h(x) dx = H(x) + C$.

Now if we take limits $\int_{a}^b h(x) dx$ that means we evaluate $H(x) +C$ at $x = b$ and at $x = a$ and subtract the result. So... $(H(b) + C) - (H(a) + C) = H(b) - H(a)$. Notice the constant (whichever value it was) "cancels out".

So we don't have to worry about the constants for specific values.

As to why you teacher said the constants were different. Your teacher was rushed, answering a common mistake, and not realizing that isn't the reason.

If you got $\frac {\cos^3 x}3 + C_1$ by method 1, and you goe $\frac{\cos^3 x}3 - \cos x + C_2$ by method 2. Something went wrong.

That would mean $\frac {\cos^3 x}3 + C_1 = \frac{\cos^3 x}3 - \cos x + C_2$ or $\cos x = C_2 - C_1$ which is a constant value. $\cos x$ is not a constant function so this can not be right.

You made an error somewhere else. Your teacher was too rushed to notice.

Answer 3

Consider $f(x)=x^2+3$. Then $f'(x)=2x$. Isn't it ? Now if integrate this $2x$ again what do I get ? I will get $x^2$. So what happened in this entire process ? I lost the "+3" in the original function. So to compensate for these losses that we add a "+c" at the end. This is just an elementary motivation. When we add limits we exactly quantify the value of "c" so it vanishes and we get the particular result. Hope this is clear.

For $\sin^3 x$ you can use the following formula directly $\sin 3x=3\sin x -4\sin^3x.$

Answer 4

Integration is just opposite of differentiation so whenever we integrate without limits we add a constant C which woud vanish on differentiating it. You can always write a function f(x) as (f(x) +0) and on integrating it, the integration of 0 is a constant ( differentiation of constant is zero) so we write a constant always beside the main answer. You can match both your answers by trignometry and you would observe that more constants come out and your both answers are same. On putting limits we actually do (g(final) +C)-(g(initial)+ C) and the constants cancel out.