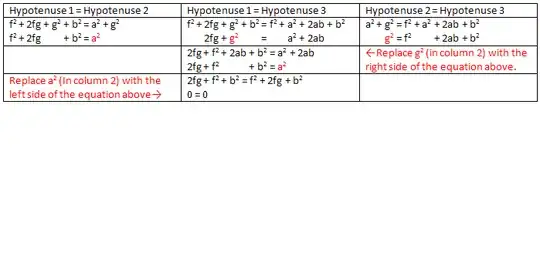
You did substitute an equation into itself, in a way. Although you have written down three equations, one of them is redundant: if $H_1, H_2, H_3$ are the lengths of the three hypotenuses, and we know $H_1 = H_2$ and $H_2 = H_3$, then $H_1 = H_3$ follows.
You've simplified two of the equations and substituted the results into the third, which yields a tautology.
The reason we only have two equations is that the system has two degrees of freedom.
- The first is scaling: if $(a,b,f,g)$ is a solution, then $(ax, bx, fx, gx)$ is also a solution.
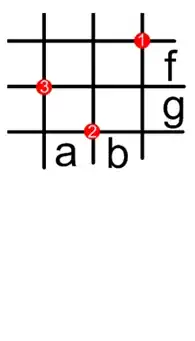
- The first is rotation: for example, if we fix vertex $3$, we can choose the angle between the $x$-axis and side $13$ of the triangle arbitrarily. (At the very least, it can vary between $0^\circ$ and $30^\circ$; past that, we'd have to draw a different diagram.)
So it makes sense to solve for two of the variables in terms of the other two. The nicest choice turns out to be to solve for $a$ and $g$ in terms of $b$ and $f$ (or vice versa), giving us (by means of equation-solving software) $$a = b + f \sqrt3, \qquad g = b \sqrt3 + f.$$
This is easier to obtain by a different argument. The vector $1\to 2$, with coordinates $(-b, -f-g)$, is a $60^\circ$ counter-clockwise rotation of the vector $1\to 3$, with coordinates $(-a-b, -f)$. So we may write down the matrix equation $$\begin{bmatrix}-b \\ -f-g\end{bmatrix} = \begin{bmatrix}\cos 60^\circ &-\sin 60^\circ \\ \sin 60^\circ & \cos 60^\circ\end{bmatrix} \begin{bmatrix}-a-b \\ -f\end{bmatrix}$$
which gives us two linear equations to solve:
$$\begin{cases} b = \frac12(a+b) - \frac{\sqrt3}{2}f \\ f+g = \frac{\sqrt3}{2}(a+b) + \frac12f\end{cases}$$
and solving for $a$ and $g$ yields the same solution.