7

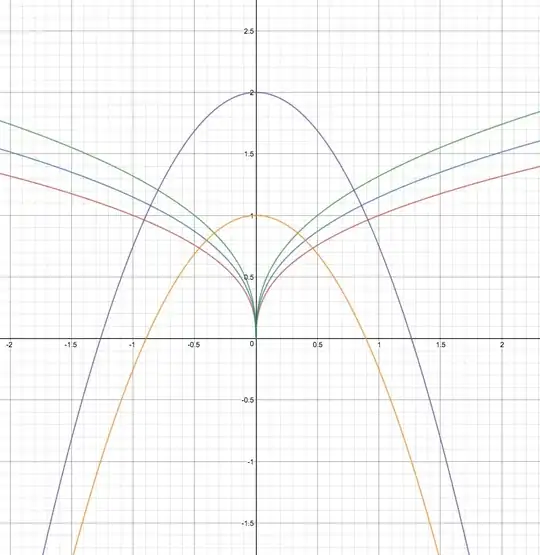
Find the orthogonal trajectories of the family of curves $y^5=kx^2$.

I start by knowing that I need a differential equation satisfying all members of family, which means $k$ needs to be eliminated.

Differentiating both sides with respect to $x$:

\begin{align*} y^5 &= kx^2\\ 5y^4 \frac{dy}{dx} &= 2kx\quad\text{Replacing }k\\ 5y^4 \frac{dy}{dx} &= 2 \frac{y^5}{x^2}x\\ \frac{5}{y} \frac{dy}{dx} &= \frac{2}{x}\\ \frac{dy}{dx} &= \frac{2}{5} \frac{y}{x} \end{align*}

Now I have a differential equation, and the orthogonal trajectory should be represented by the negative reciprocal. \begin{align*} \frac{dy}{dx}&=-\frac{5}{2}\frac{x}{y}\\ \int ydy&=\int-\frac{5}{2}xdx\\ y&=-\frac{5}{4}x^2+C \end{align*}

This equation looks orthogonal to me if I plot it, but all the valid answers are of a higher order (e.g., $y^2+\frac{5}{2}x^2=C$). There must be a gap in my understanding somewhere.

plot https://www.desmos.com/calculator/v6on063jfn

Emily Horsman
  • 361

1 Answers1

4

I made a mistake when taking $\int ydy$. It should be $\frac{y^2}{2}$ not $y$.

This means that, $$ \frac{y^2}{2}=-\frac{5}{4}x^2 + C\\ \frac{y^2}{2}+\frac{5}{4}x^2=C\\ y^2+\frac{5}{2}x^2=2C=C_2 $$

Which is the correct answer.

Emily Horsman
  • 361