I am wondering whether or not the following result is true:
For all $\varepsilon>0$, there exists infinitely many $N\in \mathbb N$ such that $$S_N:=\left\{\sum_{n=2}^N\log(n)\right\}<\varepsilon$$
where $\{\cdot\}$ denote the fractional part, i.e. $\{x\}=x-[x]$.
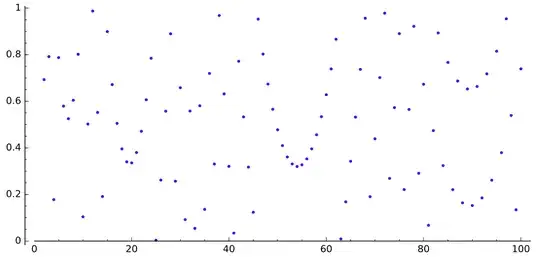
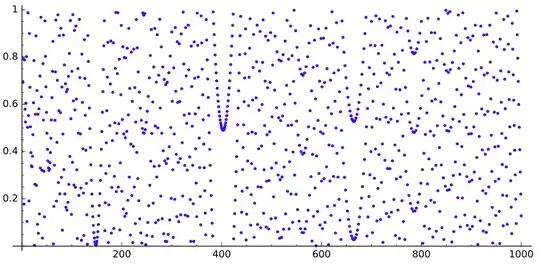
It seems to be true, looking at these drawing of $S_N$ for $N$ up to $100$ and $1\,000$ respectively. But I really don't think $1\,000$ is enough to forge an intuition regarding the veracity of the result.
I tried a comparison series-integral, to evaluation $\sum_n \log(n)$:
$$I_-=\int_2^{N-1}\log (x)\mathrm d x\leqslant \sum_{N=2}\log (n)\leqslant \int_2^{N} \log(x)\mathrm dx=I_+.$$
And we have:
\begin{align*}\int_2^k \log (x) \mathrm d x&=[(-1+\log(x))x]_2^k \\ &=(-1+\log (k))k+(1-\log 2)2,\end{align*}
so we can find an equivalent of both $I_-$ and $I_+$:
$$\begin{cases} I_-\underset{N\to\infty}\sim N\log N \\ I_+\underset{N\to\infty}\sim N\log N. \end{cases}$$
I then tried to find if $N\log(N)$ was equidistributed modulo $1$, which would prove that there is infinitely many $N$ such that $$N\log N-[N\log N]<\varepsilon.$$
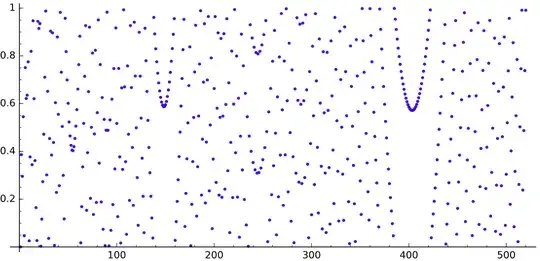
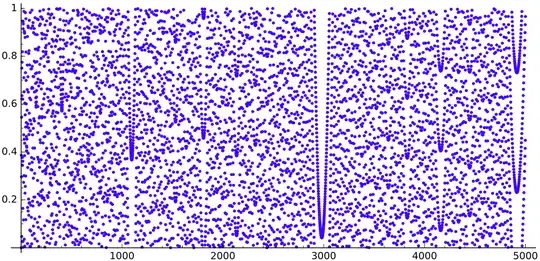
It seems true looking a these images for $N\log N$ modulo $1$ up to $520$, $5\,000$ and $30\,000$ respectively:
But I don't know how to prove it.
We win if we show that $$\lim_{N\to\infty}\frac 1N\sum_{n=1}^N e^{2\pi i \ell n\log n}=0$$
for all $\ell\in\mathbb Z\setminus \{0\}$ by Weil's criterion, but I can't prove it.
Plus, I don't think the equivalent would actually provide a proof of the result, would it?
What other approach could be taken?