Alice and Bob play the determinant game

Question

Alice and Bob play the following game with an $n \times n$ matrix, where $n$ is odd. Alice fills in one of the entries of the matrix with a real number, then Bob, then Alice and so forth until the entire matrix is filled. At the end, the determinant of the matrix is taken. If it is nonzero, Alice wins; if it is zero, Bob wins. Determine who wins playing perfect strategy each time.

When $n$ is even it's easy to see why Bob wins every time. and for $n$ equal to $3$ I have brute-forced it. Bob wins. But for $n = 5$ and above I can't see who will win on perfect strategy each time. Any clever approaches to solving this problem?

Answer 1

I tried to approach it from Leibniz formula for determinants

$$\det(A) = \sum_{\sigma \in S_n} \operatorname{sgn}(\sigma) \prod_{i=1}^n A_{i,\sigma_i}.$$

There are $n!$ factorial terms in this sum. Alice will have $\frac{n^2+1}{2}$ moves whereas Bob has $\frac{n^2-1}{2}$ moves. There are $n^2$ variables (matrix entries). Each of them taken alone appear in $(n-1)!$ terms in this summation. Whenever Bob picks a zero in his first move for any entry in the matrix, $(n-1)!$ factorial terms of this go to zero. For instance, consider a $5 \times 5$ matrix. So there are 120 terms. In first move, whenever Bob makes any matrix entry zero, he zeros out 24 of this terms. In his second move, he has to pick that matrix entry which has least number of presence in the first zeroed-out 24 terms. There can be multiple such matrix entries. In face, it can be seen that there is surely another matrix entry appearing in 24 non-zero terms in the above sum. Since $n$ is odd in this case, the last chance will always be that of Alice. Because of that, one doesn't have to bother about this terms summing to zero. What Bob has to do if he has to win is that

• He has to make sure he touches at least once (in effect zeroes) each of this 120 terms. In the $n=5$ case, he has 12 chances. In this 12 chances he has to make sure that he zeros out all this 120 terms. In one sense, It means that he has to average at least 10 terms per chance of his. I looked at the $n=3$ case, bob has 4 chances there and 6 terms, he can zero out all of them in 3 moves.

• He has to make sure that Alice doesn't get hold of all the matrix entries in one single term in 120 terms, because then it will be non-zero, and since the last chance is hers, Bob won't be able to zero it out, so she will win.

As per above explanation, in the $5 \times 5$, he has to just average killing 10 terms in each chance which seems quite easy to do. I feel this method is a bit easy to generalize and many really clever people in here can do it.

EDIT----------------

In response to @Ross Milikan, I tried to look at solving $5 \times 5$ case, this is the approach. Consider $5 \times 5$ matrix with its entries filled in by the english alphabets row-wise, so that the matrix of interest is

\begin{align} \begin{bmatrix} a & b & c & d& e \\ f& g & h &i& j \\k& l& m& n& o \\ p& q& r& s& t\\ u& v& w& x& y \end{bmatrix} \end{align}

Without loss of Generality (WLOG), let Alice pick up $a$ (making any entry zero is advantageous for her). Lets say Bob picks up $b$ (again WLOG, picking up any entry is same). This helps Bob to zero out 24 terms in the total 120. Alice has to pick up one entry in this first row itself otherwise she will be in a disadvantage (since then, Bob gets to pick the 3 terms in total from the first row and gets 72 terms zeroed out). So concerning the first row, Alice picks 3 of them, Bob picks 2 of them (say $b$ and $d$), and hence he zeros out 48 terms of the total 120. Now note that next move is Bob's. Let us swap the second column and first column. This doesn't change the determinant other than its sign. Look at the modified matrix

\begin{align} \begin{bmatrix} 0 & \otimes & \otimes & 0 & \otimes \\ g & f & h &i& j \\l& k& m& n& o \\ q& p& r& s& t\\ v& u& w& x& y \end{bmatrix} \end{align}

where $0$ is put in entries Bob has modified and $\otimes$ has been put in entries modified by Alice. Now in the first column, lets say Bob gets hold of $g$ and $q$, and alice gets hold of $l$ and $v$. Again Alice has to do this and any other move will put her in a disadvantage. Bob had made 4 moves already, the next move is his and now the matrix will look like,

\begin{align} \begin{bmatrix} 0 & \otimes & \otimes & 0 & \otimes \\ 0 & f & h &i& j \\ \otimes & k & m& n& o \\ 0 & p& r& s& t\\ \otimes & u& w& x& y \end{bmatrix} \end{align}

Now we are left with the lower $4 \times 4$ matrix, Bob is left with 8 chances, and the first move is his. Compare this with $4 \times 4$ case, it looks intuitively that Bob should win.

Answer 2

The problem states that $n$ is odd, ie., $n \geq 3$.

With Alice and Bob filling the determinant slots in turns, the objective is for Alice to obtain a non-zero determinant value and for Bob to obtain a zero determinant value.

So, Alice strives to get all rows and columns to be linearly independent of each other whereas Bob strives to get at least two rows or columns linearly dependent. Note that these are equivalent ways of saying: Obtain a non-zero determinant or a zero determinant respectively that correspond with Alice and Bob's game objectives.

Intuitively, it feels like the game is stacked against Alice because her criteria is more restrictive than Bob's. But, lets get a mathematical proof while simultaneously outlining Bob's winning strategy.

Since Alice starts the game, Bob gets the even numbered moves. So, Bob chooses $r = [r_0, r_1, \dots, r_{n-1}]$, a row vector of scalars and $c, c^T = [c_0, c_1, \dots, c_{n-1}]$, a column vector of scalars that he will use to create linear dependency relationship between vectors such that, $u \ne v, w \ne x$ and

$$r_u \times R_u + r_v \times R_v = \mathbf{0}$$ $$c_w \times C_w + c_x \times C_x = \mathbf{0}^T$$

where $\mathbf{0}$ is the row vector with all columns set to zero.

He doesn't fill $r, c$ immediately, but only when Alice makes the first move in a given column or row that is not necessarily the first move of the game (update: see Notes section. Bob decides the value for $r$ or $c$ in the last move in a pair of rows or columns). [We will shortly prove that Alice will be making the first move in any given column or row]. When Alice makes her move, Bob calculates the value of $r_v$ or $c_x$ based on the value that Alice has previously filled. Once the vector cell for $r, c$ is filled, he doesn't change it for the remainder of the game.

With this strategy in place, he strives to always play his moves (the even numbered moves in the game) ensuring that the linear dependence relation for the pair of rows (or columns) is maintained. The example below shows one of Bob's moves for rows $r_k, r_{k+1}$. Note that these could be any pair of rows, not necessarily consecutive ones. Also, this doesn't have to be a pair of rows, it also works with pairs of columns.

Bob never makes a move that fills the first cell in a row or column as part of his strategy. He always follows. Therefore, Alice is forced to make that move.

It would be impossible for Alice to beat this strategy because even if she chooses to fill a different row or column, she would be the first one to initiate the move for that row or column and Bob will follow this strategy there with the even numbered moves. It is easy to see that Alice always makes the odd numbered move in any row or column and Bob follows the even numbered move with his strategy of filling in the cell so that the linear dependence condition is met.

So, even though Alice gets the last move, Bob will make a winning move (in an earlier even numbered move) causing two rows or two columns to be linearly dependent causing the determinant to evaluate to zero regardless of what Alice does.

---

Game play for specific problem

(posed by @Misha Lavrov in comments)

The moves are numbered sequentially. Odd numbered moves are by Alice and Even numbered moves are by Bob. The 'x' and 'o' are just indicators and can be any real number filled by Alice or Bob respectively. The problem posed is for $n=5$ where Alice and Bob have made the following $4$ moves and it is Alice's turn.

Note that if Alice makes her move in any of the yellow or green cells, Bob continues with the pairing strategy described above.

The game gets interesting if Alice fills any of the blue cells. There are three possibilities:

Alice's move (type 1):

Alice fills one of the first two cells in row 5. Bob can continue the game in columns 1 and 2 and it does not matter what he or Alice fill in any of the cells in the column because Bob will need to have the last move in just one pair of rows or columns in order to win.

What happens if Alice chooses her next move outside of the first two columns? That takes us to Alice's moves - type 2 and 3.

Alice's move (type 2):

Alice can choose to fill any cell in columns $3,4$. This becomes the first cell in a pair of columns filled by Alice and Bob falls back to his following strategy.

Alice's move (type 3):

This is also similar to type 2 in that Bob uses the following strategy.

So, regardless of where Alice fills, Bob can use the following strategy to force the last move in a pair of columns or rows to be his and he can ensure that he fills the last cell in that pair with a value that ensures the pair (of rows or columns) is linearly dependent.

While the above example shows adjacent columns, Bob's strategy works for any pair of rows or columns. He ensures he always has the last move in any pair of rows or columns and hence he is guaranteed a win when he finishes any pair of rows or columns. The rest of the moves are redundant.

This is guaranteed when $n$ is odd since he always makes the second move in the game.

---

Short proof

In at least one pair of rows or columns Bob always makes the last move since he plays the second move in the game and each player alternates. Alice cannot avoid playing any pair of rows or columns completely because, Bob can fill a row or column in that pair with zeros and will win by default in $2n$ moves in that case.

Notes:

• I originally mentioned that Bob chooses $r_k$ and $c_x$ after the first move by Alice in row $k$ or column $x$. In fact, he doesn't have to make the decision until he fills the last cell in the row or column.

Answer 3

Ok so Alice has the winning strategy if the dimensions are odd, and here's why.

For Alice to win, the determinant must be non-zero, which means all rows/columns must be linearly independent.

Alice makes the first move. She can go anywhere. Then Bob makes a move. For Bob to win, in the simplest case, he needs to duplicate any one of Alice's rows or columns (then they won't be linearly independent). So his ideal strategy might be to mirror her moves. All Alice has to do is make sure Bob can't duplicate one of her rows/columns, and of course she must make sure to not duplicate any herself, but assuming she is good enough at arithmetic, this is trivial (since we can use any of the infinite real numbers)

If n were even, then Bob would win, because he could mirror Alice's moves the whole way through, and no matter where she goes, he can mirror her, right to the end, forcing one of the rows/columns to be the same as another, leading to zero determinant.

If n is odd, then this strategy no longer works for Bob, because he no longer has the last move. So even if he mirrors Alice all the way through, she can ensure that none of her rows/columns are ever duplicated by taking advantage of the odd number of rows and columns, and of the fact that she goes first and last. Ultimately, then, Alice will be able to make moves that Bob can't mirror, and so she can ensure non-zero determinant.

For example, suppose Alice is filling in a row, and Bob is mirroring her with the next row. Suppose they fill in the entire row save the final element. If alice fills this element, and Bob mirrors her, she loses. But Alice now has the whole rest of the board, so she can conceivably continue to take Bob through this process of filling in rows up to the last element. If they do this right up to the last row (since n is odd, there will be a single last row), then Alice can start filling in the last row, and Bob can no longer mirror her. Since the length of a row is odd, Alice can fill in the final element of that row. Then Bob must make a move - but the only moves available are filling in the final element of the previous rows (which come in pairs since Bob mirrored Alice all the way). But then whatever Bob picks to end a row with, Alice can choose something else for the mirror row, and thus prevent the mirrored rows from ending up as duplicates, thus maintaining independence. This goes on until the end, with Alice making the last move. Thus, Alice wins.

Answer 4

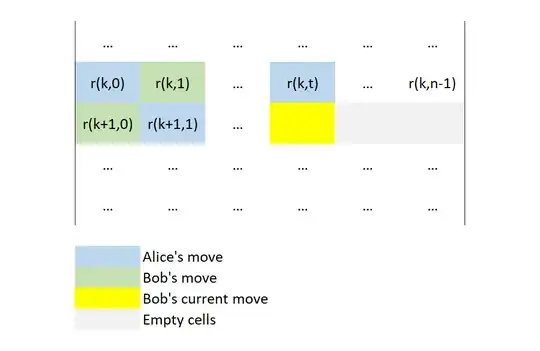
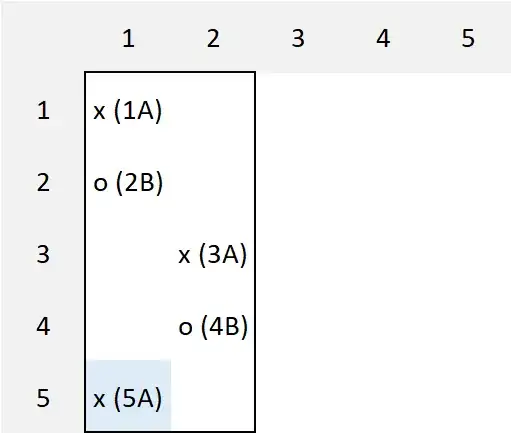
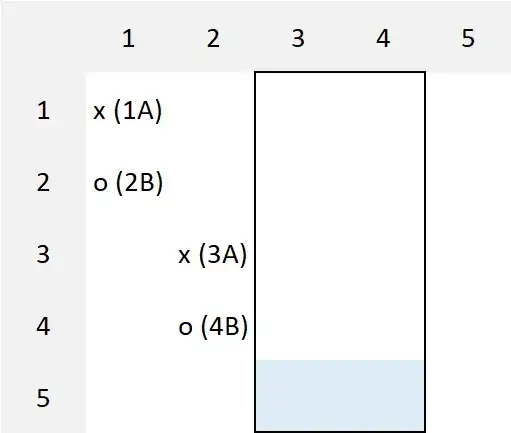
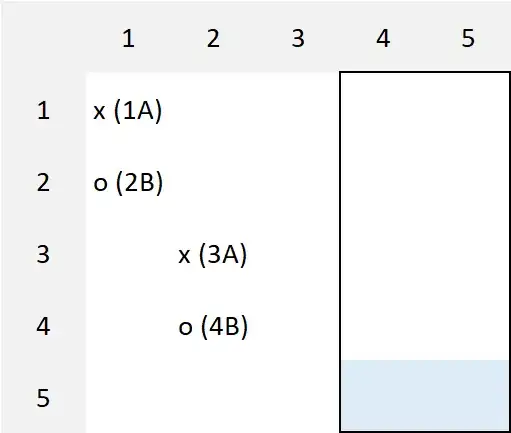
Notation.

$\blacksquare_n -\;$ unzero moves (index means the move number);

$\square_n -\;$ zero moves;

$\triangledown -\;$ threat of zero move;

$\bowtie -\;$ - the field under mutual zugzwang (counter-threats).

Idea of the such notation partially is taken from the literature of the game "go".

$\color{brown}{\textbf{Elements of the strategy.}}$

From the properties of the matrix $\;S\times S\;$ determinant follows the next.

1. Allowed matrix transformations, which hold zero/unzero determinant status:

• transposition of the matrix;
• pairwize or cyclic permutations of the rows (columns);
• order decreasing (OD), i.e. elimination of the pair "row+column", if the intersection element is the single unzero one in the filled row (column) and the quantity of undefined elements on the other line in the pair is even (if odd, then one such element should be hold to control the last move parity);
• matrix splitting (MS), by the identity $$ \begin{align} \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1m} & b_{11} & b_{12} & \cdots & b_{1n} \\ a_{21} & a_{22} & \cdots & a_{2m} & b_{21} & b_{22} & \cdots & b_{2n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mm} & b_{m1} & b_{m2} & \cdots & b_{mn} \\ 0 & 0 & \cdots & 0 & c_{11} & c_{12} & \cdots & c_{1n} \\ 0 & 0 & \cdots & 0 & c_{21} & c_{22} & \cdots & c_{2n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 0 & c_{n1} & c_{n2} & \cdots & c_{nn} \\ \end{vmatrix}\\[8pt] =\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mm} \end{vmatrix} \cdot\begin{vmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ c_{n1} & c_{n2} & \cdots & c_{nn} \\ \end{vmatrix}\end{align}\tag1 $$

2. Zero discriminant conditions, which are the threats of Z-gamer (Bob):

• zero row or column;
• MS by $(1),$ where $\;m+n > S\;$
• a pair of the proportional rows(columns).

3. Unzero discriminant condition is unzero sum of unzero terms. The threat of NZ-gamer (Alice) is to get and hold unzero terms combination.

4. Last move:

• NZ-gamer, if the matrix dimension is odd (odd case);
• Z-gamer, if the matrix dimension is even (even case).

$\qquad$ Therefore, Z-gamer wins the mutual zugzwang positions only in the even case.

5. Preferable moves of Z-gamer:

• The second zero in the same row or column ("$\square 21$"- placing) holds $\;(S-2)(S-1)!\;$ unzero terms of on $\;S\times S\;$ matrix, when the alternative moves ("$2\square11$" - placing) hold $\;(S-1)(S-1)!.$
• If the first and the second zeros are placed in one row, then the third move in the same row ("$\square31$" - placing) holds $\;(S-3)(S-1)!\;$ terms, when the placing in the vertices of a right triangle ("$\triangle22$" - placing) holds $\;(S-2)^2(S-2)!\;$ terms.
• At the next, placing ("$\square41$") holds $\;(S-4)(S-1)!\;$ terms, placing ("$\square22$") holds $\;(S-3)(S-2)(S-2)!\;$ terms, and placing ("$\triangle32$") also holds $\;(S-3)(S-2)(S-2)!\;$ terms, \begin{vmatrix} \text{Placing} & \text{Terms hold} & S=2 & S=3 & S=4 & S=5 & S=6 & S=7 \\ 2\square11 & (S-1)(S-1)! & 1 & 4 & 18 & 96 & 600 & 4320 \\ \square21 & (S-2)(S-1)! & 0 & 2 & 12 & 72 & 480 & 3600 \\ \triangle22 & (S-2)^2(S-2)! & 1 & 1 & 8 & 54 & 384 & 3000 \\ \square31 & (S-3)(S-1)! & - & 0 & 6 & 48 & 360 & 2880 \\ \square22 & (S-3)(S-2)(S-2)! & 0 & 0 & 4 & 36 & 288 & 2400 \\ \triangle32 & (S-3)(S-2)(S-2)! & - & 0 & 4 & 36 & 288 & 2400 \\ \square41 & (S-4)(S-1)! & - & - & 0 & 24 & 240 & 2160 \end{vmatrix}

6. Preferable moves of NZ-gamer:

• creating of the first unzero term (unzero moves to the intersections of the lines without unzero elements with the highest quantity of zeros) and elimination of the others (by the previous item).

Then we should collect the patterns with the predefined result.

$\color{brown}{\mathbf{2\times2\; matrices.}}$

• $ P_{20}=\begin{vmatrix} \centerdot & \centerdot \\ \centerdot & \centerdot \end{vmatrix}; \quad \color{brown}{\mathbf{ P_{20}\big|_{NZ}\Rightarrow \begin{vmatrix}\blacksquare_1 & \triangledown \\ \triangledown & \square_2 \end{vmatrix}_{NZ}\Rightarrow Z\uparrow;}}\quad; P_{20}\big|_Z\Rightarrow \begin{vmatrix}\square_1 & \triangledown \\ \triangledown & \centerdot \end{vmatrix}_{NZ}\Rightarrow Z\uparrow. $

Zero-moves of Z-gamer ($\square_1,\square_2$) create two threats ($\triangledown$), despite the first unzero move ($\blacksquare_1$) of NZ-gamer.

Result: $\color{brown}{\textbf{Force win of Z-gamer}},$ independently of the moves order.

• $P_{21}= \begin{vmatrix} \blacksquare & \triangledown \\ \triangledown & \blacksquare \end{vmatrix}\Rightarrow NZ\uparrow.$

NZ-gamer eliminates the second term and holds unzero term.

• $P_{22} = \begin{vmatrix} \blacksquare & \blacksquare \\ \bowtie & \bowtie \end{vmatrix}; \quad P_{22}\big|_{NZ}\Rightarrow Z\uparrow,\quad P_{22}\big|_{Z}\Rightarrow NZ\uparrow.$

Mutual zugzwang (MZZ) position.

Each player has the pair of the counterthreats ($\bowtie$), which allow him to control result.

If Z-player has the last move, he can provide the rows collinearness.

$\color{brown}{\mathbf{3\times3\;matrices.}}$

$P_{30} =\begin{vmatrix}\centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot \end{vmatrix},\quad P_{30}\big|_{Z} =\begin{vmatrix}\square_1 & \triangledown & \centerdot \\ \triangledown & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot \end{vmatrix}_{NZ}\Rightarrow \begin{cases} (A)\begin{vmatrix} \diagup\hspace{-14mu} \square_1 & \blacksquare_2 & \triangledown \\ \diagup\hspace{-14mu} \square_3 & \triangledown & \square_5 \\ \diagup\hspace{-14mu}\blacksquare_4 & - & - \end{vmatrix}\Rightarrow Z\uparrow\\[8pt] (B)\begin{vmatrix} \diagup\hspace{-14mu}\square_1 & \diagup\hspace{-14mu}\square_3 & \diagup\hspace{-14mu} \mathbf \blacksquare_4 \\ \triangledown & \blacksquare_2 & | \\ \square_5 & \triangledown & | \end{vmatrix}\Rightarrow Z\uparrow. \end{cases}$

The first move of Z-gamer ($\square_1$) creates two complex threats ($\triangledown$): after such move and the obvious answer at the rest field of the row (column), takes place OD to position $P_{20}\big|_{NZ}$.

Result: Z-gamer starts and wins.

$\color{brown}{\mathbf{P_{30}\big|_{NZ} \Rightarrow \begin{vmatrix} \blacksquare_1 & \bullet & \bullet \\ \centerdot & \square_2 & \bullet \\ \centerdot & \centerdot & \bullet \end{vmatrix}_{NZ}\Rightarrow \begin{cases} (A)\begin{vmatrix}\blacksquare_1 & \blacksquare_5 & \blacksquare_9 \\ \square_8 & \square_2 & \blacksquare_3 \\ \square_6 & \square_4 & \blacksquare_7 \end{vmatrix},\quad (B)\begin{vmatrix}\blacksquare_1 & \blacksquare_7 & \blacksquare_9 \\ \square_4 & \square_2 & \blacksquare_5 \\ \square_8 & \square_6 & \blacksquare_3 \end{vmatrix}\Rightarrow Z\uparrow;\\[8pt] (C)\begin{vmatrix}\blacksquare_1 & \blacksquare_3 & \blacksquare_7 \\ \blacksquare_5 & \square_2 & \square_4 \\ \blacksquare_9 & \square_8 & \square_6 \end{vmatrix},\quad (D)\begin{vmatrix}\blacksquare_1 & \blacksquare_5 & \blacksquare_3 \\ \blacksquare_7 & \square_2 & \square_6 \\ \blacksquare_9 & \square_4 & \square_8 \end{vmatrix} \Rightarrow Z\uparrow.\end{cases}}}$

Result: NZ-gamer starts, Z-gamer achieves a forced win in the all variants due to threats of $\;\square31\;$ and the final placing $\;\square22.$

$P_{31} = \begin{vmatrix} \blacksquare & \bullet & \bullet \\ \centerdot & \blacksquare & \bullet \\ \centerdot & \centerdot & \square \end{vmatrix}, \quad P_{31}\big|_{NZ} \Rightarrow \begin{cases} (A)\begin{vmatrix} \!\blacksquare\; & \bowtie & \bowtie \\ \square_4 & \!\blacksquare\; & \blacksquare_1 \\ \blacksquare_3 & \square_2 & \!\square\; \end{vmatrix},\quad (B)\begin{vmatrix} \!\blacksquare\; & \square_4 & \blacksquare_1 \\ \bowtie & \!\blacksquare\; & \bowtie \\ \square_2 & \blacksquare_3 & \!\square\; \end{vmatrix}\Rightarrow \text{MZZ};\\[8pt] (C)\begin{vmatrix} \!\blacksquare\; & \blacksquare_1 & \blacksquare_5 \\ \square_6 & \!\blacksquare\; & \square_4 \\ \square_2 & \blacksquare_3 & \!\square\; \end{vmatrix}\Rightarrow Z\uparrow. \end{cases}$

If NZ-player starts, then Z-player in the best case can achieve mutual zugzwang, and NZ-player wins.

If Z-player starts or NZ-player chooses the bad move (variant C), then Z-player wins the position.

$\color{brown}{\mathbf{4\times4\;matrices.}}$

$P_{40} =\begin{vmatrix}\centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot \end{vmatrix},\quad P_{40}\big|_{NZ} \Rightarrow P_{41} =\begin{vmatrix} \blacksquare_1 & \square_2 & \bullet & \centerdot \\ \bullet & \bullet & \bullet & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot \end{vmatrix},\quad P_{42} =\begin{vmatrix} \blacksquare_1 & \bullet & \bullet & \centerdot \\ \centerdot & \square_2 & \bullet & \centerdot \\ \centerdot & \centerdot & \bullet & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot \end{vmatrix},\quad $

$P_{41AB} =\begin{vmatrix} \blacksquare_1 & \square_2 & \scriptsize\blacksquare_3 & \centerdot \\ \scriptsize\blacksquare_3 & \square_4 & \centerdot & \centerdot \\ \centerdot & \triangledown & \centerdot & \centerdot \\ \centerdot & \triangledown & \centerdot & \centerdot \end{vmatrix} \Rightarrow Z\uparrow (\text{OD}),\quad P_{41C} =\begin{vmatrix} \blacksquare_1 & \square_2 & \centerdot & \blacksquare_{\small\text B} \\ \bowtie & \blacksquare_9 & \blacksquare_3 & \square_8 \\ \square_{\small\text C} & \square_4 & \blacksquare_7& \square_6 \\ \bowtie & \blacksquare_5 & \centerdot & \square_{\small\text A} \end{vmatrix} = Z\uparrow (\text{OD,MZZ}), $

$ P_{41D} =\begin{vmatrix} \blacksquare_1 & \square_2 & \centerdot & \blacksquare_9\\ \bowtie & \blacksquare_3 & \square_{\small\text A} & \square_8 \\ \bowtie & \blacksquare_7 & \square_4 & \square_6\\ \centerdot & \centerdot & \blacksquare_5 & \centerdot \end{vmatrix},\quad =\begin{vmatrix} \bowtie & \blacksquare_3 \\ \bowtie & \blacksquare_7 \end{vmatrix} \begin{vmatrix} \centerdot & \blacksquare_9\\ \blacksquare_5 & \centerdot \end{vmatrix} \Rightarrow Z\uparrow (\text{MS,MZZ}), $ etc.

Easily to see, that the tactic achievements of NZ-player crushes on the mutual zugzwang.

$\color{brown}{\mathbf{5\times5\;matrices.}}$

$ P_{50}\big|_{NZ} =\begin{vmatrix} \centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \centerdot & \centerdot & \centerdot & \centerdot \end{vmatrix}\big|_{NZ}\Rightarrow \begin{vmatrix} \blacksquare_1 & \centerdot & \centerdot & \centerdot & \centerdot \\ \centerdot & \square_2 & \blacksquare_3 & \blacksquare_9 & \centerdot \\ \centerdot & \square_4 & \centerdot & \square_6 & \blacksquare_7 \\ \centerdot & \blacksquare_5 & \centerdot & \centerdot & \centerdot \\ \centerdot & \bowtie & \bowtie & \square_8 & \centerdot \end{vmatrix}\Rightarrow NZ\uparrow (\text{MZZ}). $

NZ-player wins, due to the last move and essentially greater choice of the useful moves.

Should expect, that the considered factors should hold, and the last move provides the victory, if $\;\mathbf{S>3.}$

Answer 5

This is a sequential game type. Both players act one after each other. The players are aware of the decisions the other player did in his last action. The information if perfect for the player starting the game and partially perfect for the opponent. That is based on the fast that the opponent has to take into account that only zeros and or hidden number can bring him the win, making the determinant of the matrix zero. The appropriate method to represent this game is the extensive form. The representation is a Rooted tree with order.

n is the order, rank of the matrix:

n=1: Alice starts with a real number and always wins.

n=3: Alice starts and whatever field she is selected we can permute it to be the uppermost leftmost. Since determinants change by permuting odd and even times only by sign, this is easily achieved. Now is Bobs turn and for sure he will select the rightmost lowermost field. Alice fills in the last field on the diagonal and Bob puts a zero in one of the fields neighboring his first field entry. Then Alice fills that row or column with her next real. Bob fills the remaining neighboring field of the matrix to his first entry and then Alice the last field.

The problem reduces to the equivalent one of selecting 4 matrix elements and setting them zero or making a nonzero determinant matrix a zero determinant matrix in maximal 4 steps if Alices was not the opponent. But only three steps are needed to do that.

All other matrices of this kind can be created by permutations in row and, or column.

Alice can choose her strategies and the goal of the game is win.

One determinant calculated with a filled 3D matrix like following the above procedure is

-Subscript[a, 1, 3] Subscript[a, 2, 2] Subscript[a, 3, 1] + Subscript[a, 1, 1] Subscript[a, 2, 2] Subscript[a, 3, 3]

In general: If two rows of a matrix are equal, its determinant is zero. This is because of property 2, the exchange rule. On the one hand, exchanging the two identical rows does not change the determinant.

But that not really matter in this game.

Which is for sure unequal zero, because Alice never will choose to enter a zero. Four zeros oppose five reals in the Matrix. That suffices always that Alice will win. Bob can only have two neighboring entries and never a full row. He can never fill two zero on the diagonal if Alice is clever enough.

The determinant of a matrix filled in the above manner will be a product of three of Alice's entry, sometimes a sum or difference of two such products.

Alice will have (^2+1)/2 moves whereas Bob has (^2−1)2 moves. So Alice always has the first and the last step in filling the matrix. Lets again start the filling. We can always reorder the columns and rows in a way that Alice starts to the uppermost leftmost field. Then Bob has his filling. And so one. Before a first judgment is possible at least more that one row or column is.

The simple case is that Bob was able to fill a complete row or column with zeros. The most probable variation of a checkerboard filling leads together with the development rule of the determinant. The more mixed the entries of Alice and Bob are the easier the calculation of our determinant gets.

Alice may for example choose to enumerate her entries ascending or descending does not matter.

The step for proving this for n odd to m odd is not as easy as it seems. We need two new rows and columns every step. Since the checkerboard pattern is always easily achieved for Alice this is no problem. Would the checkerboard pattern be inaccessible for Alice this step will fail! But it is as can be verified for each n independent of odd or even.

How looks the decision tree for Alice?

Top step: Alice has the choice of 9 matrix element: probability 1/9 each.

Second step: Bob has the choice of 8 matrix element: probability 1/8 each.

...

So the last step is the ninth step with the probility 1/9!.

There are 9! nodes in the ninth step.

Because of the strategy this a priori probabilites loose their meaning. Such that Alice never chhoses zero as input or all the same numbers.

Answer 6

We know that the determinant of a matrix A is non-zero if the rank of the matrix is the same size of the matrix. So, in this case, rank(A) is odd. So, on the last column (or first column) all Alice has to do to guarantee a win is make sure the real number cannot be written as a linear combination of the others in that column, thereby making every column independent. This in turn makes the rank(A) = n, which is to say the determinant is non-zero.

May not be the correct answer as to what you are looking for, but it is a generalized result.