The following text is from the book A Friendly Introduction to Number Theory by J H Goldenman :)
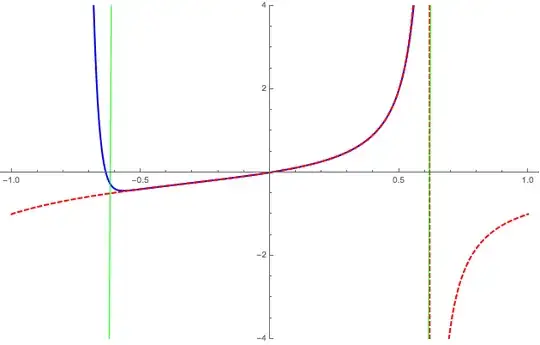
Checking the process again and again I found no restriction for x (i.e. the area of convergence). However, for x=1 we have $\infty = -1$. When we say $1+x+x^2+ \dots = \dfrac{1}{1-x}$, valid for $|x|<1$, that's becasue $1+x+x^2+ \dots + x^n = \dfrac{1-x^{n+1}}{1-x}$ for any $x$, then we impose $-1<x<1$ in order to make the series convergent for $n \to \infty$; But how the l.h.s of Fibonacci Generating Function Formula doesn't show divergence when written in a close form?