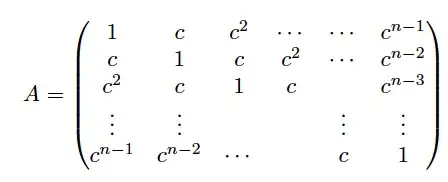Determinant of a Gram's $n \times n$ matrix

Question

If I have a $n \times n$ matrix, call it A, and I know that the determinant of the matrix $A_{n-1,n-1}>0$, how can I prove that det($A_{n,n})>0$, for the following special case? The idea is to prove, by induction, that $A$ is a positive-definite matrix.

I would also want to know which are the vectors $v_{i}$, $v_{j}$ that satisfy $(v_{i}|v_{j})=c^{|i-j|}$ i.e I would also want to find the set of independent (normalized) vectors that have $A$ for Gram's matrix.

Note: $0<c<1$.

I don't see how the matrix is relevant to the last question. — Asinomás, Feb 21 '17 at 20:08
It's easy to see that $A$ will be positive definite in the case that $\frac{c}{1 - c} < 1 \implies c < 1/2$. I don't see how to approach the general case, though. — Ben Grossmann, Feb 21 '17 at 20:15
@JorgeFernándezHidalgo please, you can see now the final question. Tank you — Sergi, Feb 21 '17 at 20:15
@MartinR I think you did not see the note. c<1, so what you say is not possible — Sergi, Feb 21 '17 at 20:17
@Sergi note that in this case, $A$ is diagonally dominant. This won't lead to a general approach. I'll try something else, first. — Ben Grossmann, Feb 21 '17 at 20:18

score 5 · Answer 1 · edited Feb 21 '17 at 21:08

5

Substracting from rows $2$ to $n$ the previous row multiplied with $c$ leaves you with an upper triangular matrix, and the determinant is the product of the diagonal elements $$ 1 \cdot (1-c^2) \cdots (1-c^2) = (1-c^2)^{n-1} $$ which is positive for $0 < c < 1$.

edited Feb 21 '17 at 21:08

darij grinberg

19,173

answered Feb 21 '17 at 20:26

Martin R

128,226

1

+1. The same argument works in greater generality: See Theorem 1 in http://math.stackexchange.com/questions/1383741/is-this-determinant-always-non-negative/1384516#1384516 – darij grinberg Feb 21 '17 at 21:04
hello. Thank you for your anawer. Do you have any idea about how to find de eigenvalues of A in the general case? – Sergi Feb 27 '17 at 14:30

user1551 · Accepted Answer · 2017-02-24T21:55:21.633

4

Let $N$ be the upper triangular nilpotent Jordan block of size $n$. Then $$ (I-cN)\,A\,(I-cN)^T=\operatorname{diag}(1-c^2,\ldots,1-c^2,1)\succ0. $$ Therefore $A$ is positive definite, by Sylvester's law of inertia. Furthermore, we may rewrite the above as $A=V^TV$, where $$ V=\operatorname{diag}\left(\sqrt{1-c^2},\ldots,\sqrt{1-c^2},1\right)\left((I-cN)^{-1}\right)^T. $$ Hence the columns of $V$ satisfy $\langle v_i,v_j\rangle=a_{ij}=c^{|i-j|}$. More specifically, $V$ is the lower triangular matrix given by $$ v_{ij}=\begin{cases} 0 &\text{ if }j>i,\\ \sqrt{1-c^2}c^{i-j} &\text{ if }j\le i<n,\\ c^{n-j} &\text{ if }j\le i=n. \end{cases} $$

edited Feb 24 '17 at 21:55

answered Feb 21 '17 at 20:48

user1551

149,263

Hello, is the decomposition of $A=V^{T}V$ unique? and why? i.e I would want to know if the decomposition of a self-adjoint operator in terms of $A^{\dagger}A$ is unique. thank you. @user1551 – Sergi Feb 24 '17 at 17:31
@Sergi If $A=V^TV$, then $A=(QV)^T(QV)$ for every real orthogonal matrix $Q$. So, the decomposition is not unique in general. – user1551 Feb 24 '17 at 17:48
thank you for both answers. What I have not understood about your firs answer is: what are the set of vectors ${v_{i}}$ that satisfy $( v_{i} | v_{j} )=c^{|i-j|}$ – Sergi Feb 24 '17 at 18:18
sorry but I do not understand this notation... If you post a more specific expression for $v_i$ I will be very thankfuly. – Sergi Feb 24 '17 at 20:49
diag$(\cdot)$ it has no sense for me, does it mean a diagonal $n \times n$ matrix with eigenvalues $\sqrt{1-c^2}$ and 1? And also i have no knowledege about "triangular nilpotent Jordan block of size $n$". But I do not want it to be a problem for you. It is okay... – Sergi Feb 24 '17 at 23:09
@Sergi $\operatorname{diag}(d_1,d_2,\ldots,d_n)$ means a diagonal matrix whose diagonal entries are $d_1,d_2,\ldots,d_n$. An upper triangular nilpotent Jordan block (note: what I wrote is "upper triangular", not just "triangular" --- a nilpotent Jordan block is always triangular) means a matrix that has ones on its first super-diagonal and zeroes elsewhere. That is,$$N=\pmatrix{0&1\ &0&1\ &&\ddots&\ddots\ &&&0&1\ &&&&0}.$$ – user1551 Feb 25 '17 at 07:43
@Sergi By the way, I was a bit irritated that you had accepted my answer without even understanding the first line. I apologise if I've been rude in my comments. Anyway, I hope I have fully answered your question now. – user1551 Feb 25 '17 at 08:09
yes, perfect. Thank you very much. Good luck – Sergi Feb 25 '17 at 09:04
hello. Do you have any idea about how to find de eigenvalues of A in the case n=100? (last question) – Sergi Feb 27 '17 at 14:29
@Sergi I'm not aware of any closed-form formula, but this and also this MO threads may be relevant. If you want to find the smaller eigenvalues numerically, beware that $A$ is very ill-conditioned, because of the presence of $(I-cN)^{-1}$. – user1551 Feb 27 '17 at 15:28
yes... I should find the eigenvalues numerically. Thank you very much! – Sergi Feb 27 '17 at 16:54

score 2 · Answer 3 · answered Feb 21 '17 at 20:28

2

By induction: the base case $n=1$ is easy. In general: write $$ A_n = \pmatrix{1 & x^T\\x&A_{n-1}} $$ Now, compute the Schur complement $$ A_n/A_{n-1} = 1 - x^TA_{n-1}^{-1}x $$ However, $x$ is simply the first column of $A_{n-1}$ multiplied by $c$. Thus, we have $$ A_n/A_{n-1} = 1 - x^T[A_{n-1}^{-1}x] = 1 - c\;x^Te_1 = 1 - c^2 $$ Because $A_{n-1}$ and $A_n/A_{n-1}$ are both positive (definite), we can conclude that $A_n$ is positive definite.

answered Feb 21 '17 at 20:28

Ben Grossmann

234,171
12
184
355

hello. Thank you for your anawer. Do you have any idea about how to find de eigenvalues of A in the general case? – Sergi Feb 27 '17 at 13:57
No idea, sorry. – Ben Grossmann Feb 27 '17 at 14:11

Determinant of a Gram's $n \times n$ matrix

3 Answers3