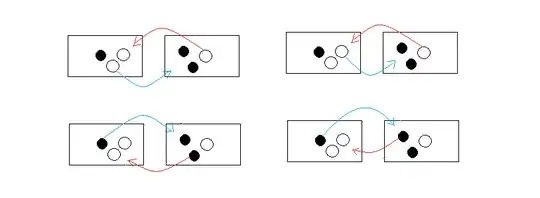
Three white and three black balls are distributed in two urns in such a way that each contains three balls. We say that the system is in state i, i = 0, 1, 2, 3, if the first urn contains i white balls. At each step, we draw one ball from each urn and place the ball drawn from the first urn into the second, and conversely with the ball from the second urn.
Let $X_n$ denote the state of the system after nth step. Now how to prove that $(X_n=0,1,2,...)$is a markov chain and how to calculate its transition probability matrix.
Solution:If at the initial stage both the urns have three balls each and we draw one ball from each urn and place them into urn different from the urn from which it is drawn. So after nth step state of the system will be 3 and it will remain it forever. So this is not a markov chain. I also want to understand the meaning of bold line.
If I am wrong, explain me why and how I am wrong and what is the transition matrix of this markov chain. Would any one answer this question?