Convergence of a sequence

Question

$$\huge{{\sqrt2},{\sqrt2}^{\sqrt2},{\sqrt2}^{{\sqrt2}^{\sqrt2}},{\sqrt2}^{{\sqrt2}^{\sqrt2^{\sqrt2}}},\cdots}$$ I want to show the sequence converges to $2$

First I plot $f(x)=\displaystyle{\sqrt2}^x ,g(x)=x$, this figure show me $f(x)=g(x)$ has two root $x=2,4$ then plot $\displaystyle y={\sqrt2},{\sqrt2}^{\sqrt2},{\sqrt2}^{\sqrt2^{\sqrt2}},...$ show me that $x=2 $ is convergence point . If I write ${\sqrt2}^x=x$ then put $x$ in l.h.s I will have ${\sqrt2}^{\sqrt2^x}=x$ so this is my way $$\displaystyle{{\sqrt2}^x=x\\{\sqrt2}^{{\sqrt2}^x}=x\\ {\sqrt2}^{{\sqrt2}^{{\sqrt2}^{x}}}=x\\ {\sqrt2}^{{\sqrt2}^{{\sqrt2}^{{\sqrt2}^{x}}}}=x\\\vdots \\{\sqrt2}^{{\sqrt2}^{{\sqrt2}^{{\sqrt2}^{\cdots}}}}=x\to 2}$$

$$$$ (1) Am I right ?
(2)Is there another method to find convergence ?

Thanks In advanced.

Answer 1

From Paul Halmos's "Problems for Mathematician Young and Old":

There is really only one sensible interpretation of the three dots in ${\sqrt2}^{{\sqrt2}^{{\sqrt2}^{{\sqrt2}^{\cdots}}}}$ that indicate that the tower should be continued indefinitely, namely as a limit. What is meant is that we should form finite towers such as ${\sqrt2}^{{\sqrt2}^{{\sqrt2}^{{\sqrt2}^{\cdots^{\sqrt2}}}}}$.

make them higher and higher, and then try to let the heights tend to infinity. More explicitly: write $x_1$ =$\sqrt2$, and then, for every positive integer n, define $x_{n+1}$ as ${\sqrt2}^{x_n}$ ; the question is whether or not the sequence {$x_n$} converges, and, if so, to what. The natural guess would seem to be no---how could it converge?

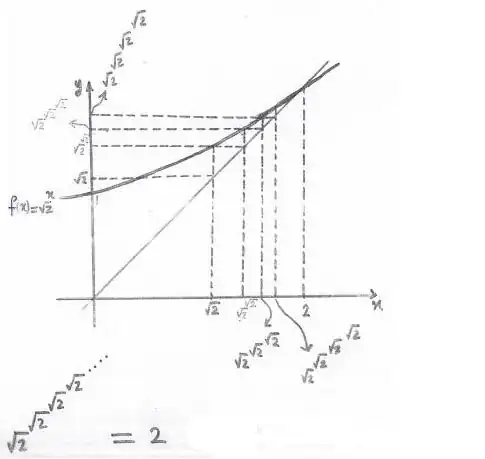
One question is obviously relevant: what kind of a function of x does the expression ${\sqrt2}^x $define? Answer: a monotone increasing function. That is: if x < y, then ${\sqrt2}^x $<${\sqrt2}^y $. Isn't that clear? If there is any doubt about it, take the logarithm of both sides of the inequality, or, more precisely, look at the result of forming that logarithm, agree that it's a correct statement, and then form its exponential.

Two consequences follow from the monotone increasing character of ${\sqrt2}^x $. One is that the sequence ${x_n}$ is increasing (an obvious induction), and the other is that the sequence is bounded from above by 2. To see the latter consequence, replace the topmost ${\sqrt2} $ in the tower ${\sqrt2}^{{\sqrt2}^{{\sqrt2}^{{\sqrt2}^{\cdots^{\sqrt2}}}}}$

by 2, thus getting a larger number, and observe that the result telescopes downward. (That is, replace what are now the top two exponents, namely ${\sqrt2}^2$, by the value they give, namely 2, and then continue downward.) These two consequences imply the conclusion: the sequence ${x_n}$ is convergent to some limit less than or equal to 2. Can that limit be evaluated? Sure-easy. Call it t, so that t=lim $x_n$. It follows that

${\sqrt2}^t$=${\sqrt2}^{lim x_n}$=lim ${\sqrt2}^{x_n}$=$lim x_{n+1 }$=$lim x_n$=t

or, throwing away the steps and keeping only the conclusion, ${\sqrt2}^t$= t.

This equation can be solved by inspection: it has the obvious solutions 2 and 4. The latter is not possible, because we already know that t $\leqq2$...so the conclusion is that t = 2

Answer 2

The sequence generated by $a_0=\sqrt{2}$ and $a_{n+1}=\sqrt{2}^{a_n}$ is increasing and $a_n<2$ ensures $a_{n+1}<2$, hence it is bounded and convergent to its supremum. The limit point has to fulfill $L=\sqrt{2}^L$ and $L\leq 2$, hence the limit is $\color{red}{2}$ as expected.

Answer 3

$x={\sqrt2}^{{\sqrt2}^{\sqrt2^{\sqrt2}}}\cdots$

$\implies x={\sqrt2}^x$

$\implies x={2}^{x/2}$

For $x=2,$ $\text{LHS}=\text{RHS}=2$

Note: ignoring $4$ because the answer must be less than $ 2$