Find $ \max \Im(W(- \exp(x)) \exp(-x) ) $ for real $x$.

Question

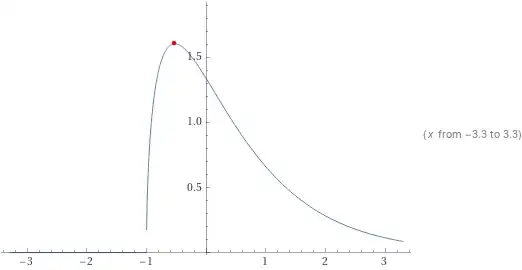
Define the reals $x,y$ as

$$ y = \max \Im ( W ( - \exp(x)) \exp(-x) ) $$

$W$ is the standard Lambert $W$ function and $\Im$ is the imaginary part.

How do we find $x$ and $y$?

Closed forms (allowing integrals, sums, etc), contour integrals, numerical methods?

I know how to express the local COMPLEX max on the complex plane for an analytic function by a contour integral.

I also know the Cauchy-Riemann equations that relate an analytic function's real and imaginary parts by differential equations.

Yet, this does not appear to help me. Maybe it should help me, but I do not know how.

I ask here for a case of the $W$ function, because i do not want to ask too General questions. But I am also interested in general methods of course.

Answer 1

$\DeclareMathOperator WW \DeclareMathOperator {Im}{Im}\DeclareMathOperator{sinc}{sinc}$We find an inverse function for $\Im(\W(-e^x))$. Taking the real and imaginary parts of $z=\W(-e^x)\iff(a+bi)e^{a+b i}=-e^x$ shows:

$$\begin{cases}ae^a\cos(b)-be^a\sin(b)=-e^x\\ae^a\sin(b)+be^a\cos(b)=0\iff a=-b\cot(b)\end{cases}$$

substituting gives $\ln(b\csc(b))-b\cot(b)=x,b=\Im(\W(-e^x))$. Now we differentiate and use $\frac{df^{-1}(x)}{dx}=\frac1{f’(f^{-1}(x))}$:

$$\frac d{dx}e^{-x}\Im(\W(-e^x))=e^{-x}\left(\frac b{1-2b\cot(b)+b^2\csc^2(b)}-b\right)=0\iff \sin(2b)=b$$

This search gives posts solving $\sin(2b)=b$ and we see $b=\Im(\W(-e^x))=\frac12\sinc^{-1}(\frac12)$ with the inverse sinc function. An answer in the post shows:

$$\sin(2b)=b\implies b=\frac{2\pi}{\pi+4}+\frac2\pi\sum_{n=1}^\infty\sum_{m\in\Bbb Z}\frac{(-1)^mJ_m\left(\frac{4\pi n}{\pi+4}\right)\cos\left(\frac\pi2\left(\frac{2\pi n}{\pi+4}-m\right)\right)\sin\left(\frac{2\pi^2n}{\pi+4}\right)}{n\left(1-\left(\frac{2\pi n}{\pi+4}-m\right)^2\right)}$$ shown here with the input and output only:

Burniston and Siewert also give an integral representation. Therefore :

$$\boxed{y=\max(e^{-x}\Im(\W(-e^x)))= 1.604559655\dots,x=-0.5265169098\dots\\\text{at}\left(\ln(b)\csc(b)-b\cot(b),\sin(b)e^{b\cot(b)}\right)}$$

with $b$ defined above. The maximum is plotted here: