Quantify the similarity between two patterns formed by two sets of spatial locations

Question

Suppose I have two sets of spatial locations $X$ and $Y$ on the plane, each with $n$ locations. The coordinates are $X=\{(x_1, y_1), \dots, (x_n, y_n)\}$ and $Y=\{(u_1, v_1), \dots, (u_n, v_n)\}$. I want to find a quantity representing the similarity between the two patterns formed by those locations.

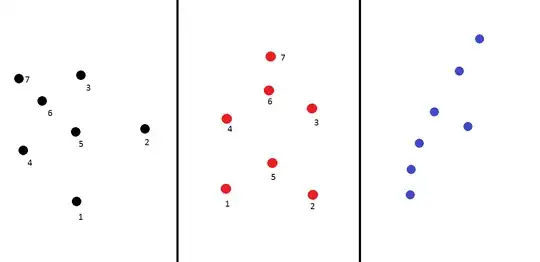
For example, in the figure below, the pattern by black dots are apparently more similar to the one by the red dots than the blue dots. But that's subjective. I wonder if there is a reasonable way to define a quantity which will take a larger value if two patterns are more similar and a small value if they are very different.

This quantity should have the following properties:

• It does not depend on the scale. One pattern can be large, e.g., the pattern of the stars in the sky; the other one could be small, e.g., the pattern of trees in your backyard. You are free to proportionally rescale the pattern.
• It does not depend on the orientation. In the figure, I can rotate the red dots by an appropriate angle first and then compare with the black pattern.
• It does not depend on the absolute location which means I can freely move the pattern around by a translation before comparing.

Here is what I did so far. Since the rotation in 2D can be represented by a matrix $$T=\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin \theta & \cos \theta\end{pmatrix}\, ,$$ scaling can be represented by the multiplication of a constant $a$, and translation can be represented by adding a constant two-dimensional vector $\mathbf{b}=(b_1, b_2)$. I can first transform the second pattern $Y$ as $$Y'=aTY + \mathbf{b}\, .$$ After that, I define a distance between the two patterns $X$ and $Y'$ as $$D=\| X-Y'\| ^2=\sum_{i=1}^{n}[(x_i-u'_i)^2+(y_i-v'_i)^2]$$ Since $D$ is a function of $a, \theta, b_1, b_2$, I can minimize $D$ to the optimal parameters $\hat{a}, \hat{\theta}, \hat{b}_1, \hat{b}_2$.

Here is a question I have. When computing $D$, I have to pair those locations, black 1 with red 1, black 2 with red 2, etc. However, that is subjective already. Is there an automatic way of doing this? Or, is there a better way of doing the whole thing?

Answer 1

So first off, you've stated the problem very well. I think this belongs to a general class of problems concerning the comparison of point clouds. There are a number of ways in which people do this, but there is a paper that I like in particular, which is along the lines of what you have already been thinking about:

https://graphics.stanford.edu/courses/cs468-05-winter/Papers/PCD/guille_PCDcomp.pdf

the above work is directly concerned with point cloud comparison, while a related work:

http://sites.fas.harvard.edu/~cs277/papers/gromov.pdf

is concerned with general shape comparison. Both of these works can be fairly technical in places but I think they are pretty readable overall. The basic idea (as I'm sure you can tell from the title) is that the authors use the Gromov-Hausdorff distance as means of comparison between two 'sets'. This is the idea that we compare these things, not just as sets, but as metric spaces which can be embedded in a larger metric space. Now we are able to look at the 'distance' between these two sets in a way which accounts for all possible isometric transformations (think the inf of the 'set distance' over all possible isometric transformations). This way of approaching the problem is nice for a number of reasons: it generalizes very easily to comparisons of point clods on n-dimensional manifolds, and it gives you some freedom to decide what metric you want to use to decide similarity. Hope this helps!