6

Update:
(because of the length of the question, I put an update at the top)
I appreciate recommendations regarding the alternative proofs. However, the main emphasis of my question is about the correctness of the reasoning in the 8th case of the provided proof (with a diagram).

Original question:

I would like to know, whether the following proof, is a valid way to prove that $a^2 + b^2 \neq 3c^2$ for all $a, b, c \in Z$ (except the trivial case, when $a=b=c=0$). More formally, we have to prove the correctness of the following statement:

$$P: (\forall a,b,c \in Z, a^2 + b^2 \neq 3c^2 \lor (a=b=c=0))$$

Proof. (by contradiction)
For the sake of contradiction let's assume, that there exist such $a, b, c \in Z$, that $a^2 + b^2 = 3c^2$ (and the combination of $a,b,c$ is not a trivial case). More, formally, let's assume that $\neg P$ is true:

$$\neg P: (\exists a,b,c \in Z, a^2 + b^2 = 3c^2 \land \neg (a=b=c=0))$$

There are $2^3$ possible combinations of different parities of $a,b,c$ (8 disjoint cases, which cover entire $Z^3$). So, in order to prove the original statement, we have to consider each case, and show that the true-ness of the $\neg P$ always leads to some sort of contradiction.

Let's consider 8 possible cases (7 of which are simple, whereas the 8th case looks a bit intricate, and I am not sure regarding its correctness):

Case 1) $a$ is odd, $b$ is odd, $c$ is odd
Thus:
$a = (2x + 1)$, $b = (2y + 1)$, $c = (2z + 1)$ for some $x, y, z \in Z$
So:
$$ a^2 + b^2 = 3c^2 \\ \implies (2x + 1) ^2 + (2y + 1)^2 = 3 \cdot (2z + 1)^2 \\ \implies 2 \cdot (2x^2 + 2x + 2y^2 + 2y + 1) = 2 \cdot (6z^2 + 6z + 1) + 1 \\ \implies even\ number = odd\ number \\ $$

However, the derived result contradicts to the fact that odd numbers and even numbers can't be equal. Hence: $(even\ number = odd\ number) \land (even\ number \neq odd\ number)$, or equivalently: $(even\ number = odd\ number) \land \neg (even\ number = odd\ number)$. Contradiction.

Case 2) $a$ is odd, $b$ is odd, $c$ is even
Thus:
$a = (2x + 1)$, $b = (2y + 1)$, $c = 2z$ for some $x, y, z \in Z$
So:
$$ a^2 + b^2 = 3c^2 \\ \implies (2x + 1) ^2 + (2y + 1)^2 = 3 \cdot (2z)^2 \\ \implies 2 \cdot (2x^2 + 2x + 2y^2 + 2y + 1) = 12z^2 \\ \implies 2 \cdot (x^2 + x + y^2 + y) + 1 = 6z^2 \\ \implies odd\ number = even\ number $$ Contradiction.

Case 3) $a$ is odd, $b$ is even, $c$ is odd
Thus:
$a = (2x + 1)$, $b = 2y$, $c = (2z + 1)$ for some $x, y, z \in Z$
So:
$$ a^2 + b^2 = 3c^2 \\ \implies (2x + 1) ^2 + (2y)^2 = 3 \cdot (2z + 1)^2 \\ \implies 4x^2 + 4x + 1 + 4y^2 = 12z^2 + 12z + 3 \\ \implies 4\cdot(x^2 + x + y^2) = 2 \cdot (6z^2 + 6z + 1) \\ \implies 2\cdot(x^2 + x + y^2) = 6z^2 + 6z + 1 \\ \implies even\ number = odd\ number $$ Contradiction.

Case 4) $a$ is odd, $b$ is even, $c$ is even
The square of an odd number is odd (so, $a^2$ is odd).
The square of an even number is even (so, $b^2$ and $3c^2$ are even).
Fact: the sum of an even number and an odd number is odd.
However, equality: $a^2 + b^2 = 3c^2$ leads to the conclusion, that: $odd\ number + even\ number = even\ number$
Contradiction.

Case 5) $a$ is even, $b$ is odd, $c$ is odd
Symmetric to the Case 3 (because $a$ and $b$ are mutually exchangeable), which shows the contradiction.

Case 6) $a$ is even, $b$ is odd, $c$ is even
Symmetric to the Case 4, which shows the contradiction.

Case 7) $a$ is even, $b$ is even, $c$ is odd
Thus:
$a = 2x$, $b = 2y$, $c = (2z + 1)$ for some $x, y, z \in Z$
So:
$$ a^2 + b^2 = 3c^2 \\ \implies 4x^2 + 4y^2 = 12z^2 + 12z + 3 \\ \implies even\ number = odd\ number $$ Contradiction.

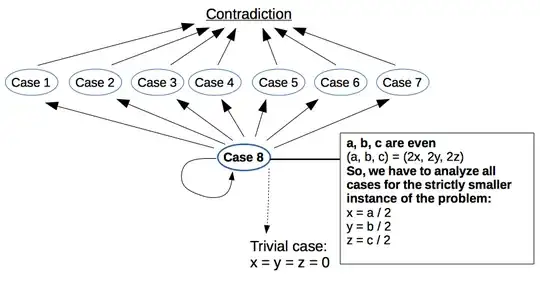
Case 8) $a$ is even, $b$ is even, $c$ is even
Thus:
$a = 2x$, $b = 2y$, $c = 2z$ for some $x, y, z \in Z$
So: $$ a^2 + b^2 = 3c^2 \\ \implies 4x^2 + 4y^2 = 3 \cdot 4z^2 \\ \implies x^2 + y^2 = 3z^2 $$

Now, we are faced with the similar instance of the problem, however, the size of the problem is strictly smaller ($x = {a \over 2}$, $y = {b \over 2}$, $z = {c \over 2}$).
At first glance, it seems that we have to consider again the eight possible parities of $x, y, z$. However, if we analyze all dependencies between the cases of the problem, we will notice that the only possible outcomes are either contradiction or the trivial case:

enter image description here

We have shown the contradiction in all cases, hence we have subsequently proved the original statement. $\blacksquare$

So, I would like to know, if there is any problem with reasoning in the 8th case?

stemm
  • 220
  • $+1$ for the diagram! (and overall well-presented question) –  Jan 22 '17 at 19:11
  • Everything is very cumbersome. And if the equation will be different? Or is it proof specifically for a single equation? The solvability of quadratic forms is reduced to finding the solvability of some equivalent of Pell's equation. Take the formula and find out when it has at least one full rate. http://math.stackexchange.com/questions/1513733/solving-a-diophantine-equation-of-the-form-x2-ay2-byz-cz2-with-the-co/1514030#1514030 – individ Jan 23 '17 at 04:21
  • @individ, thank you for your advice. I fully agree with you regarding the usefulness of solving the general case of the problem. However, the main accent of my question is focused on the correctness of the reasoning in the 8th case of the provided proof (with a diagram). I would like to know, if there are any flaws in the reasoning inside the 8th case. – stemm Jan 23 '17 at 20:57
  • Anyone can ask a question. You specify the form of the solution. You equation is not solved. Why did you decide that the form of the solution needs to look like this? Maybe the solution needs to have a different view? If there is a solution you can always obtain another by multiplying or dividing by a common divisor. What is the evidence? The equations to be solved, rather than guessing what the solution might be. – individ Jan 24 '17 at 04:17
  • @individ as I have already pointed, the main emphasis of the question is on the correctness of reasoning in the 8th case of the presented proof. Was that a correct logical step - to rely on the graph of dependencies between the cases of the proof? If yes, I would appreciate the references to examples of other proofs, which make use of a similar technique. If approach is wrong, I would like to know the reason why. – stemm Jan 24 '17 at 07:45
  • This approach is not correct because does not contain proof. Is some form - and why it is considered the solutions have this form? For such cases, use modular arithmetic. The criterion of solvability proposed by Legendre. It is necessary to use if there is a need to prove. https://ru.wikipedia.org/wiki/Теорема_Лежандра – individ Jan 24 '17 at 11:45
  • @individ proposed approach does contain the proof by contradiction. The original statement: $P: (\forall x,y \in Z, a^2+b^2 \neq 3c^2)$. For the sake of contradiction it is assumed that $\neg P$ is true. So: $\neg P: (\exists x,y \in Z, a^2+b^2=3c^2)$. Each integer can be either odd or even, hence there are possible $2^3$ disjoint combinations of $a,b,c$. Afterwards it is shown, that every possible combination of parities leads to the contradiction. Which, subsequently implies that $\neg P$ is false, which contradicts to the initial assumption. QED. – stemm Jan 24 '17 at 13:21
  • In this case, it should work for other coefficients, but it will not. For the other example of Prime numbers would not work. – individ Jan 24 '17 at 13:26
  • @individ for other coefficients it might not work, because you won't be able to show the contradiction for some combinations of parities of $a,b,c$ (you will obtain tautologies instead). – stemm Jan 24 '17 at 13:29
  • I have noticed the typo in one of my previous comments. There should have been written: $P: (\forall a,b,c \in Z, a^2+b^2 \neq 3c^2)$ and $\neg P: (\exists a,b,c \in Z, a^2+b^2=3c^2)$ – stemm Jan 24 '17 at 13:34
  • May say that I consider this evidence - and it's still this will not be considered. Actually rewrote one equation into another form. And then just said - there are none. There is generally no evidence. Where is it? How can there be proof if I say - there's an even number then they are not even? – individ Jan 24 '17 at 13:57
  • @individ this is the essence of how the proof by contradiction works: it is assumed that the logical statement $\neg P(a,b,c)$ is true, than it is shown, that the further reasoning (constructed on the top of $\neg P(a,b,c)$) leads to an any sort of contradiction. If we have shown the contradiction for all possible values of $a,b,c$, then we have subsequently shown that the initial assumption is wrong, hence $P(a,b,c)$ is true. – stemm Jan 24 '17 at 14:50
  • It is not proof. You are not the first who is trying to do. Take the equation rewrite it in another form, and then you say that none. – individ Jan 24 '17 at 15:11
  • @individ have you read the original problem? "Prove, that $P$ is true, $P: (\forall a,b,c \in Z, a^2+b^2 \neq 3c^2)$". The proof is not about rewriting the equation. At the beginning of the proof it is assumed that $\neg P$ is true. And afterwards, it is shown that such assumption leads to the nonsense. Which is the target of the proof by contradiction. – stemm Jan 24 '17 at 15:22
  • How else do you explain the language? When solving equations like this. And in this form of replacement. Formally, the numbers themselves must be rational. Because knowing one solution can be to other division and multiplication by the common divisor. The concept of parity is not applicable - because there is formally a rational number. I'm tired of arguing. You don't want to listen. – individ Jan 24 '17 at 16:02
  • @individ where do you see rational numbers in a following piece of the proof? Case 1) Let $a=(2x+1),\ b=(2y+1),\ c=(2z+1)$ for some $x,y,z \in Z$. Assuming that $a^2+b^2=3c^2$ is true, the values of $a,b,c$ are substituded accordingly: $(2x+1)^2+(2y+1)^2=3 \cdot (2z+1)^2$, which leads to the following expression: $2 \cdot (2x^2 + 2x + 2y^2 + 2y + 1) = 2 \cdot (6z^2 + 6z + 1) + 1$ which is obviously false $\forall x,y,z \in Z$. In a similar way, it is shown the contradiction for all other combinations of parities of $a,b,c$ - which covers entire $Z^3$. Please, read carefully the question. – stemm Jan 24 '17 at 16:12

2 Answers2

2

Suppose a solution with at least one of $a,b\neq 0$ exists. If $(a,b,c)$ is a solution then $(\frac{a}{\gcd(a,b)},\frac{b}{\gcd(a,b)},\frac{c}{\gcd(a,b)})$ is also a solution (and all terms are integers), and $a$ and $b$ are coprime.

Now notice that $a^2+b^2$ cannot be a multiple of $3$ unless both are multiples of $3$ (because $a^2\equiv 0$ or $1\bmod 3$). We conclude that if $a^2+b^2=3c^2$ we have $a=b=0$.

Asinomás
  • 107,565
  • 1
    This proof is basically infinite descent, only that instead of using infinite descent we prove that a coprime solution must exist if a non-trivial solution exists. – Asinomás Jan 22 '17 at 19:16
  • Jorge Fernández Hidalgo, thank you for the suggested proof. However, I would really appreciate any comments regarding the correctness of the proof, which described in the question. – stemm Jan 29 '17 at 16:43
  • where does $(a,b)\mid c$ come from? :o – AlvinL Aug 02 '19 at 19:08
  • You have to prove it but it is pretty straight forward – Asinomás Aug 03 '19 at 00:20
  • @JorgeFernándezHidalgo Well, that's why I asked, doesn't look that obvious at all. We could analyse two cases: $(3,c^2) =1$ and $(3,c^2)=3$, but it's not clear cut. How do you approach this? – AlvinL Aug 03 '19 at 08:10
  • An alternative solution is to note $v_3(a^2+b^2)$ is even and $v_3(3c^2)$ is odd. – Asinomás Aug 03 '19 at 21:54
  • @JorgeFernándezHidalgo how is $v_3$ defined? – AlvinL Aug 04 '19 at 08:06
  • The maximum power of 3 that divides the number – Asinomás Aug 04 '19 at 19:59
2

There is truth in your method for case 8. It is called inifinte descent and equivalent to induction (i.e., alternatively you might start away with assuming that $(a,b,c)$ is the smallest non-trivial solution, and then $(a/2,b/2,c/2)$ cannot be a solution).

Hagen von Eitzen
  • 382,479