Lyapunov stability

Question

i have a question regarding Lyapunov stability and basin of attraction.
Let

$${x}'=-x-y$$ $${y}'=2x-y+y^3$$ Use $$V(x,y)=x^{2}+\frac{1}{2}y^{2}$$ to determine the stability of (0,0) and a basin of attraction.
We have $$\dot{V}(x,y)=2x(-x-y)+y(2x-y+y^3)$$ or $$\dot{V}(x,y)=-2x^2-y^2+y^4$$. Now

1. V is positive definite and continuously differentiable
2. V(0,0)=0

Now,$$\dot{V}(x,y)$$ is negative definite if $$-y^2+y^4<0$$ or
$$-1<y<1$$ . Now the textbook says that in order for $$x^{2}+\frac{1}{2}y^{2}=c$$ to stay in the strip $$ \kappa = \left \{ \right.(x,y):x \in R,y \in (-1,1) \left. \right \}$$ it must hold true that $$c\in (0,1/2)$$.
This is where i stuck ,i don't understand the last step from which he concluded that $$c\in (0,1/2)$$.Can someone help me?

Answer 1

$$ % f(x) = % \left[ \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right] % = % \left[ \begin{array}{c} -x -y \\ 2x - y + y^{3} \end{array} \right] % $$

Before looking at the Lyapunov function, let's take a peek at the phase portrait. The red dashed line represents $\dot{x} = 0$, purple $\dot{y}=0.$

The critical points are the origin and $(\pm \sqrt{3}, \mp \sqrt{3})$

---

Lyapunov function $$ V(x,y) = x^{2} + \frac{1}{2} y^{2} $$ Gradient of Lyapunov function $$ \nabla V = \left[ \begin{array}{c} 2x \\ y \end{array} \right] $$ Time derivative $$ \dot{V} = \nabla V \cdot f = \left[ \begin{array}{c} 2x \\ y \end{array} \right] \cdot \left[ \begin{array}{c} -x -y \\ 2x - y + y^{3} \end{array} \right] = -2x^{2} - y^{2} + y^{4} $$ This function is shown below. The red contour line is the $\dot{V}=0$ contour. The region between these two red lines is the region where $\dot{V}<0$. The band for $-1 < y < 1$ is now apparent.

Answer 2

This problem can be handled with an optimization procedure, having in mind that generally is a non convex problem. The result depends on the test Lyapunov function used so we will generalize to a quadratic Lyapunov function

$$ V(p) = p^{\dagger}\cdot M\cdot p = a x^2+b x y + c y^2,\ \ \ p = (x,y)^{\dagger} $$

and

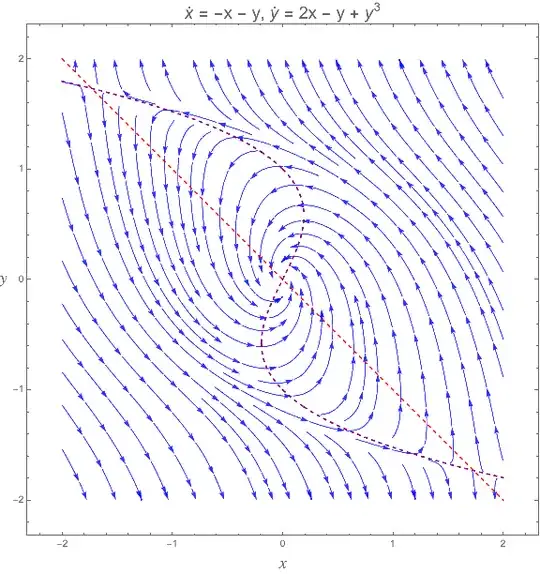
$$ f(p) = \{-x - y, 2 x - y + y^3\} $$ with $a>0,c>0, a b-b^2 > 0$ to assure positivity on $M$. We will assure a set involving the origin $Q_{\dot V}$ such that $\dot V(Q_{\dot V}) < 0$. The optimization process will be used to guarantee a maximal $Q_{\dot V}$.

After determination of $\dot V = 2 p^{\dagger}\cdot M\cdot f(p)$ we follow with a change of variables

$$ \cases{ x = r\cos\theta\\ y = r\sin\theta } $$

so $\dot V = \dot L(a,b,c,r,\theta)$. The next step is to make a sweep on $\theta$ calculating

$$ S(a,b,c, r)=\{\dot V(a,b,c,r,k\Delta\theta\},\ \ k = 0,\cdots, \frac{2\pi}{\Delta\theta} $$

and then the optimization formulation follows as

$$ \max_{a,b,c,r}r\ \ \ \ \text{s. t.}\ \ \ \ a > 0, c> 0, a c -b^2 > 0, \max S(a,b,c,r) \le -\gamma $$

with $\gamma > 0$ a margin control number.

Follows a MATHEMATICA script which implements this procedure in the present case.

f = {-x - y, 2 x - y + y^3};
V = a x^2 + 2 b x y + c y^2;
dV = Grad[V, {x, y}].f /. {x -> r Cos[t], y -> r Sin[t]};
rest = Max[Table[dV, {t, -Pi, Pi, Pi/30}]] < -0.5;
rests = Join[{rest}, {r > 0, a > 0, c > 0, a c - b^2 > 0}];
sols = NMinimize[Join[{-r}, rests], {a, b, c, r}, Method -> "DifferentialEvolution"]
rest /. sols[[2]]
dV0 = Grad[V, p].f /. sols[[2]]
V0 = V /. sols[[2]]
r0 = 2;
rmax = r /. sols[[2]];
gr0 = StreamPlot[f, {x, -r0, r0}, {y, -r0, r0}];
gr1a = ContourPlot[dV0, {x, -r0, r0}, {y, -r0, r0}, ContourShading -> None, Contours -> 80];
gr1b = ContourPlot[dV0 == 0, {x, -r0, r0}, {y, -r0, r0}, ContourStyle -> Blue];
gr2 = ContourPlot[x^2 + y^2 == rmax^2, {x, -r0, r0}, {y, -r0, r0}, ContourStyle -> {Red, Dashed}];
Show[gr0, gr1a, gr1b, gr2]

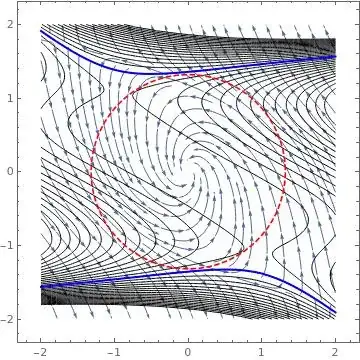
Follows a plot showing in black the level sets $Q_{\dot V}$ an in blue the trace of $\dot V = 0$. In dashed red is shown the largest circular set $\delta = 1.31977$ defining the maximum attraction basin for the given test Lyapunov function's family.