6

There is a binary distinction between rational and irrational numbers: all real numbers can either be expressed as $p/q$ for integer $p$ and $q$, or they can't. This question was inspired by the thought that, while some irrational numbers are 'almost' rational in the sense of being very close to a rational number of low denominator; other rational numbers are 'almost' irrational in the sense of requiring a very large denominator.

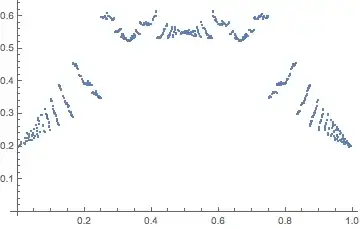
Let $r$ be a real number between $0$ and $1$. To calculate $r$’s ‘irrationality score’, that is $S(r)$, we take the following procedure.

  1. Find the distance between $r$ and the closest rational number with denominator $1$ (that is, an integer). Add this value $\min \{r, 1-r\}$ to the score.

  2. Next, calculate the minimum distance between $r$ and the closest rational number with denominator $2$. If this is smaller than the score achieved in step $1$ (i.e. $r$ can be better approximated by $1/2$ that by $0$ or $1$), then add this distance to the total score.

  3. Repeat the procedure for rational numbers with denominator $3$; then $4$ and so on. If any score is smaller than the smallest score achieved previously, add it to the total score.

For a rational number $r$, by definition there will be a finite number of steps, as once the denominator is equal to $q$, the rational approximation is perfect and no better approximation can be made.

Of course, for an irrational $r$, there are infinite additions to make to calculate its score, though these converge rapidly. For instance, for $r = \pi - 3$, the best approximations are: $0/1; 1/3; 1/4; 1/5; 1/6; 1/7; 8/57 \dots $ It's score is approximately $0.34$.

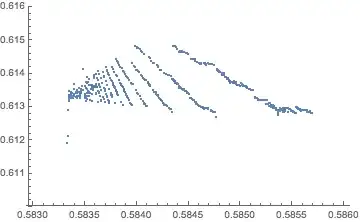
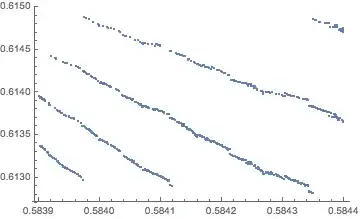
It is provable that $S(k/q) \to (\ln 2 – 0.5)$. As $q \to \infty$, for any $k$.

There are, however, several questions to ask:

What value of $r$ maximizes $S(r)$?

What is the expected value of $S(r)$ if $r$ is a randomly generated number between $0$ and $1$?

Mason
  • 4,489
Thomas Delaney
  • 1,803
  • I'm a bit confused by your description. What is $S(\frac{1}{2})$? – Chas Brown Jan 12 '17 at 07:51
  • S(1/2)=1/2. This is because for q=1 both 0/1 and 1/1 are half away from r - in this case .5 - and then when q=2 the best approximation of 1/2 is equal to r, thus yielding a score of zero. As any subsequent score is only added to S(r) if it is less that the previous best approximation, which in this case is 0, nothing will be added and thus S(r)= 1/2+0=1/2. – Thomas Delaney Jan 12 '17 at 08:27
  • Related: https://math.stackexchange.com/questions/1090142/how-can-we-measure-how-irrational-a-number-is – Klangen Jun 21 '18 at 16:32

2 Answers2

4

Some data: The largest score I can find, by random trial and error, is $S(0.5839751641596652) \approx 0.6148779$. There's another slighly lower peak around $r=0.732$. Here are a few graphs of random samples.

full graph

medium zoom

close-up

Greg Martin
  • 92,241
0

(notes: apologies for hyperlinks instead of images, I don't have enough rep to post images yet apparently)

The current answer provided some really interesting visuals, it inspired me to attempt it myself and to uncover some more information on this topic.

Firstly, the mean value of $S(r)$ seems to be $\mu_S ≈ 0.4361$ The image shows the evolution of the mean over time, as well as the empirical mean.

mean values

However, clearly this sample mean may not be a good representation to the expected value. Plotting the distribution shows that the chance of actually obtaining a score around $\mu_S$ may be lower than expected.

Here are my results for estimating the distribution of the score using kernel estimation methods: Kernel Estimates for Bandwidth Kernel Estimation Methods

Also, interestingly obvious from the visuals are the clear cuts found at the point of the more simple real fractions (1/2,2/3,3/4):

fractional cuts

(d = recursion depths & ss = sample_size)

Jack Thompson
  • 1