A many population $U$ has many elements $u_i$, each of which has some associated value of interest $x_i$ which can be measured precisely. The values of $x$ are distributed according to a Gaussian distribution. For the purposes of this question, it can be assumed that this is a unit normal distribution because the answer to the question will not depend on the underlying mean or variance.
Two experimenters, $E_1$ and $E_2$, are interested in determining the population mean value $<x>$. $E_1$ obtains $n>1$ samples from $U$, computes the mean, and computes a 95% confidence interval, of length $I_1$ centered on that estimated mean. $I_1$ is of course proportional to the standard error of the sample that $Ee_1$ obtained.
$E_2$ does exactly the same experiment as $E_1$, except that she uses twice the sample size: $2n$ samples. It is, of course, likely that $I_2 < I_1$, but that is not certain.
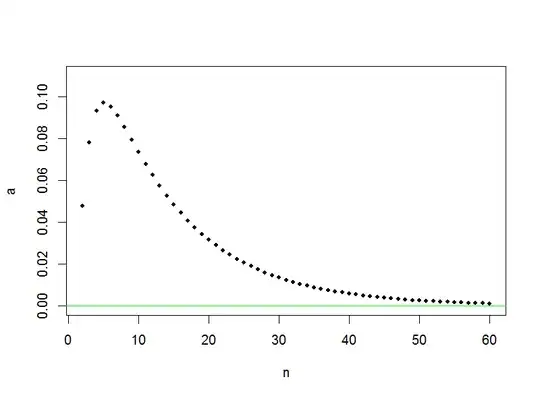
What is the probability $A(n)$ that $I_1 < I_2$?
That is meant to ask how rapidly does $A(n)$ fall with $n$.