17

Let the sequence $\{a_{n}\}$ be such that $a_{1}=1, a_{2}=100$, and $$a_{n+2}=\left\lceil \dfrac{4}{3}a_{n+1}-a_{n}+0.5\right\rceil$$

Prove that the sequence $\{a_{n}\}$ is periodic.

I have used a computer and found the periodic is $T=874$, but how to prove it?

VIVID
  • 11,667
math110
  • 94,932
  • 17
  • 148
  • 519
  • 2
    If I am not mistaken, then the period is in fact 2204, since $(a_{2205}, a_{2206}) = (1, 100)$ and no such pattern between 1 and 2205. – Sangchul Lee Jan 06 '17 at 17:29
  • 1
    You are correct: $(a_1,,a_2) = (1,,100) = (a_{1+2204},,a_{2+2204})$. Nevertheless, it seems that this case is not something exceptional. It is most likely that for every starting pair $(a_1,,a_2)$, the resulting sequence is periodic! At least this is true for for all cases ${-100 \le a_1,a_2 \le +100}$. For example, corresponding to the question period, we have: $(a_1,,a_2) = (1,,99) = (a_{1+874},,a_{2+874})$. – Hazem Orabi Jan 09 '17 at 09:46
  • I'm confused. Didn't Sangchul already give a proof? You can compute $(a_{2205},a_{2206}) = (1,100)$, and then that tells you the sequence is periodic. – mathworker21 Dec 29 '20 at 13:53
  • 1
    If two consecutive terms determine the next term, also if we have already observe 874 is a period, then we are done. Maybe an interesting question is whether we can remove brute force computation to find the same. – Sungjin Kim Dec 30 '20 at 20:17
  • 2
    Could you reveal where does this problem come from? – VIVID Jan 04 '21 at 20:04

2 Answers2

13

This is not an answer, but rather an observation.

The following graph shows the set of points $P = \{(a_n, a_{n+1}) : n \geq 1\}$.

$\hspace{8em}$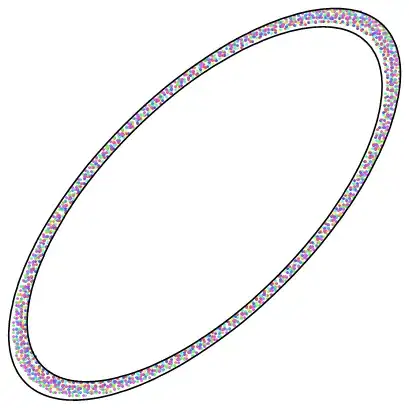enter image description here

Notice that they are confined in a very narrow region and are clustered near an ellipse. This ellipse is not hard to identify. Indeed, if a sequence $(b_n)$ satisfies

$$ b_{n+2} = \frac{4}{3}b_{n+1} - b_n, $$

then it follows that

$$ \det \begin{pmatrix} b_{n+1} & b_n \\ b_{n+2} & b_{n+1} \end{pmatrix} = b_{n+1}^2 - \frac{4}{3}b_{n+1}b_n + b_n^2 $$

is constant, since

$$ \begin{pmatrix} b_{n+2} & b_{n+1} \\ b_{n+3} & b_{n+2} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -1 & \frac{4}{3} \end{pmatrix} \begin{pmatrix} b_{n+1} & b_n \\ b_{n+2} & b_{n+1} \end{pmatrix} \quad \text{and} \quad \det \begin{pmatrix} 0 & 1 \\ -1 & \frac{4}{3} \end{pmatrix} = 1. $$

Thus the points $(b_n, b_{n+1})$ stays forever on the ellipse

$$f(x, y) := x^2 - \frac{4}{3}xy + y^2 = \text{const}.$$

If we can somehow show that $f(a_n, a_{n+1})$ is also bounded by some perturbation argument, then since the region $f(x, y) \leq c$ is bounded and $P$ has only integer points, we can argue that $(a_n)$ is eventually periodic. But at this point, I am not sure if this observation will be really useful.

VIVID
  • 11,667
Sangchul Lee
  • 181,930
  • 3
    Nice plot. Mind sharing the code you used ? – Gabriel Romon Jan 06 '17 at 18:40
  • 1
    @LeGrandDODOM, Unfortunately I neither saved nor remember the code exactly. But it was a Mathematica code that looked like this: l = NestList[{#[[2]], Ceiling[4/3 #[[2]] - #[[1]] + 1/2]} &, {1, 100}, 2204]; Show[Graphics[Point /@ l]] – Sangchul Lee Jan 06 '17 at 18:43
0

N.B. This is not complete answer, but just extrapolation of the clue provided by @SangchulLee.

First of all we can rewrite the recurrence as:

$$a_{n+2}=\frac{4a_{n+1}}{3}-a_{n}+v_{n+1}$$ where $$v_{n+1}=\begin{cases} 1 & a_{n+1} = 0 \bmod 3\\ \frac{2}{3} & a_{n+1} = 1 \bmod 3 \\ \frac{4}{3} & a_{n+1} = 2 \bmod 3 \end{cases}$$

Now we define $$A_{n} = \begin{bmatrix} a_{n+1} & a_{n} \\ a_{n+2} & a_{n+1} \end{bmatrix}$$ $$B = \begin{bmatrix} 0&1 \\ -1&\frac{4}{3} \end{bmatrix}$$ $$U_1 = \begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix}$$

$$U_2 = \begin{bmatrix} 0&0 \\ 1&0 \end{bmatrix}$$ This means $$A_{n+1} = BA_{n}+v_{n+1}U_1+v_{n+2}U_2$$ Then we can write $$\det(A_{n+1}-v_{n+2}U_2) = \det(A_{n}+v_{n+1}B^{-1}U_1) $$

Simplifying this one obtains $$a_{n+2}^2-\frac{4a_{n+2}a_{n+1}}{3}+a_{n+1}^2-v_{n+1}(a_{n+2}+a_{n+1}) = a_{n+1}^2-\frac{4a_{n+1}a_n}{3}+a_n^2-v_{n+1}(a_{n+1}+a_n)$$

Notice that the equation $x^2-4xy/3+y^2-v(x+y)=C$ represents an ellipse for a given constant $C$ and $v\in\{1,2/3,4/3\}$

I was not able to proceed from here! Hope this helps although its a little late!

Coniferous
  • 810