6

Let $C\subset\mathbb{R}^n$ non-empty. Its polar set $C^\circ$ is defiend as $$C^\circ\equiv \{y\in \mathbb{R}^n\mid \forall x\in C, \,\,\langle y,x\rangle \le 1 \},$$ where $\langle\cdot,\cdot\rangle$ denotes the Euclidean inner product.

I cannot think of an example of a set and its polar set in $\mathbb{R}^2$. What is a good example of a set and its polar set?

glS
  • 7,963
fidel castro
  • 567

2 Answers2

11

A few examples include:

  1. The polar set of a singleton $\{x\}$ is a halfspace with support hyperplane orthogonal to $x$. If $\|x\|=1$ then the halfspace touches $x$, otherwise its below $x$ iff $\|x\|>1$:

$\hspace{40pt}$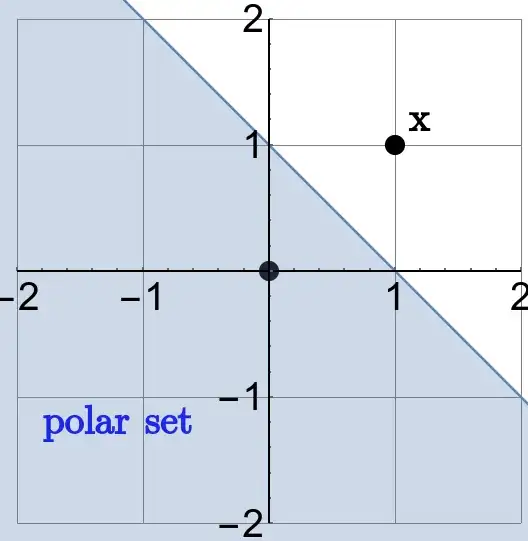

  1. The polar set of a unit disk is the disk itself.

  2. See this question for the polar set of $\{(x,y)\in\mathbb R^2: x^2+y^4\le1\}$.

  3. Consider the polytope with the four vertices $(\pm 1,\pm1)$ (a square centred at the origin). Then its polar set is a rotated square with vertices $(0,\pm1),(\pm1,0)$: $\hspace{40pt}$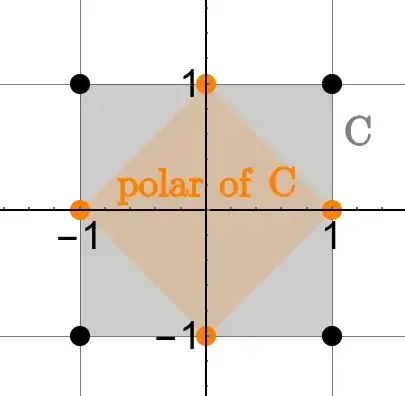

  4. You can find more examples in these lecture notes by Jonathan Kelner (Link to pdf).

If you have access to Mathematica, I made a simple snippet to explore how the polar sets of finite numbers of points look like. Just click anywhere to add points and see the corresponding polar set:

$\hspace{40pt}$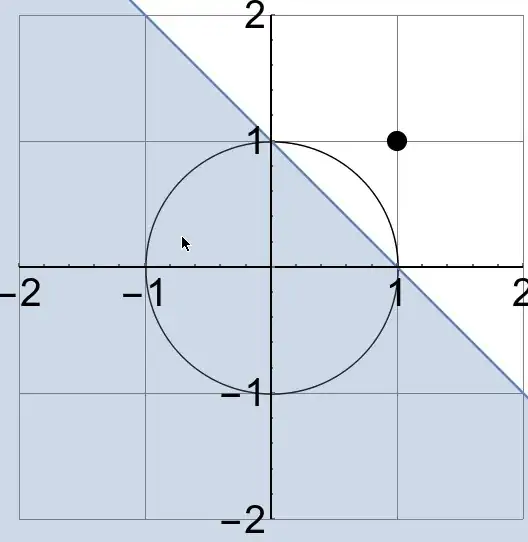

Here's the code to generate this visualisation:

DynamicModule[{pts={{1,1}}},
    EventHandler[
        Dynamic@Show[
            Graphics[{
                PointSize@0.04,Dynamic@Point@pts,
                Circle[]
            },
                Axes->True,AxesOrigin->{0,0},Frame->False,PlotRange->ConstantArray[{-2,2},2],
                GridLines->Automatic,AxesStyle->Directive[Large,Black]
            ],
            RegionPlot[
                And@@(Dot[#,{x,y}]<=1&/@pts),
                {x,-4,4},{y,-4,4},PlotPoints->50
            ]
        ],
        {"MouseClicked":>(AppendTo[pts,MousePosition["Graphics"]])}
    ]
]

See source of this answer for the MMA code used to generate the figures.

glS
  • 7,963
4

The basic example given by LinAlg in the comments is the key to understanding polar sets in general: when $C=\{c\}$ is just a point, then $$ C^\circ = \{\, y\in\mathbb R^n \,|\, \langle y, c\rangle \le 1\,\} =: H_c $$ is a half-space with the boundary hyperplanes outward normal direction being the direction of $c$ and distance from the origin given by $1/\|c\|$.

Using this, we can express polar sets in the following way for arbitrary $C\subseteq \mathbb R^n$: $$ C^\circ = \{ \,y\in \mathbb R^n \,|\, \forall c\in C\colon y\in H_c\,\} = \bigcap_{c\in C} H_c. $$ Hence, the polar set is an intersection of all the half-spaces $H_c$ where $c$ ranges over the points in $C$.

Christoph
  • 25,552