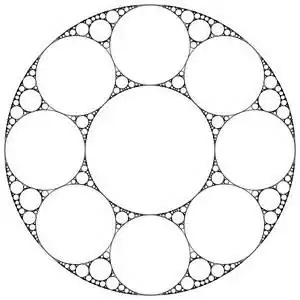
Let's say that the radius of the outer circle is 5 and the radius of the largest circle in the Apollonian gasket is 3(both from the center of the outer circle) This would mean 8 circles of radius 2 right?
What I get for calculating the area within the circles of the Apollonian gasket(assuming we go no further than the circles of radius 2) is this equation:
$$πR_{c}^{2} - (πR_{c}^{2} - (πr_{l}^{2} + 8*πr_{s}^{2})) = Area$$
where $πR_{c}^{2}$ is the area of the outer circle, $πr_{l}^{2}$ is the area of the largest inner circle, and $πr_{s}^{2}$ is the area of the smallest inner circle we are considering.
So with the radii given I get this:
$$25π - (25π - (9π + 32π)) = Area$$
$$25π - (25π - 41π) = Area$$
$$25π - (-16π) = Area$$
$$41π = Area$$
So obviously something is wrong with my area formula because if I have a circle of radius 5, no matter how many circles I have in there, the area cannot be any bigger than $25π$.
So where am I wrong? I mean the term in the outer parentheses is supposed to represent the area of the Apollonian gasket not covered by the inner circles and the term in the inner parentheses is supposed to represent the area of the inner circles.