Is a function which preserves zero and affine lines necessarily linear?

Question

My question is directly inspired by this other recent question, but I was trying to figure out whether or not it holds for $\mathbb R$. This led me to two questions. Let $n \ge 2$ be an integer (we're not including $n = 1$ as there are trivial counterexamples in dimension $1$).

1. Let $V$ and $W$ be real vector spaces, both of dimension $n$, and let $f: V \to W$ be a bijection which sends zero to zero and affine lines to affine lines. Is $f$ necessarily linear?

2. Let $V$ be a real vector space of dimension $n$. If we forget the vector space structure on $V$, and remember only the data of what the affine lines in $V$ are and $n$, can we recover the topology on $V$?

An affirmative to question 1 implies an affirmative to question 2: Simply choose any bijection $f: V \to \mathbb R^n$ which preserves affine lines, and $f$ is necessarily a homeomorphism.

In dimension $n=2$, question $2$ is equivalent to the following problem:

• Using only the data of what the affine lines are, given $3$ distinct parallel lines (which can be characterized as those which don't intersect with each other), determine which line is in the middle.

Once you know that, you can describe open sets in terms of the unions of lines between two parallel lines.

Similarly, for $n=2$, question 2 is also equivalent to:

• Using only the data of what the affine lines are, given a line and $3$ distinct points, determine which point is in the middle.

It would also be good to know whether, and how, the answers to 1 and 2 depend on the dimension of $V$.

Answer 1

I'll provide an outline of a proof - thanks to Moishe Cohen and Christian Sievers for providing some of the hints.

Theorem: Let $F$ be any field with at least $3$ elements, let $V$ and $W$ be vector spaces over $F$, both of dimension $\ge 2$, and let $f: V \to W$ be a bijection which sends $0$ to $0$ and affine lines to affine lines. Then $f$ is semi-linear, that is, there is an automorphism $\phi: F \to F$ such that $f(av+w) = \phi(a)f(v)+f(w)$, for every $v, w \in V$ and $a \in F$.

In the case of $F = \mathbb R$, there are no nontrivial automorphisms, so every such bijection is linear.

Of course, the presense of $0$ is a minor technicality; it enables the easy use of linear algebra. Without $0$, every map is "semi-affine".

In the following outline, there is good Euclidean Geometric intuition for $F = \mathbb R$, but all steps can be carried out algebraically for arbitrary fields.

1. Affine planes in $V$ can be characterized as follows: For two lines $L_1$ and $L_2$ which intersect at a unique point, their affine span $A$ is the union of the two lines with all lines $L$ which intersect $L_1$ and $L_2$ at distinct points. This is the step that requires $|F| \ge 3$; everything after hinges only on knowing what the affine lines and affine planes and $0$ are.

2. We can therefore characterize parallel lines: They are the pairs of lines which are disjoint and lie in the same affine plane.

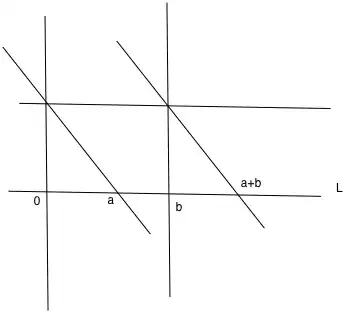
3. We can characterize addition: If $v$ and $w$ are linearly independent, then denote by $L_v$ and $L_w$ the lines which go through $0$ and $v$, and $0$ and $w$ respectively. Let $L_v'$ be the line parallel to $L_v$ which passes through $w$, and let $L_w'$ be the line parallel to $L_w$ which passes through $v$. Then $v+w$ is the unique point in the intersection of $L_v'$ and $L_w'$. Furthermore, $(-w)$ can be characterized by $(v+w)+(-w) = v$. Then for $v'$ linearly dependent with $v$, $v+v' = ((v+w)+v')+(-w)$.

4. For nonzero vectors $v$, denote $L_v$ as in 3. For linearly independent $v$ and $w$, we can characterize the bijection $L_v \to L_w$ given by $a v \mapsto a w$, for each $a \in F$. Explicitly, $aw$ is the intersection with $L_w$ of the line through $av$ which is parallel to the line passing through $v$ and $w$.

5. For $v'$ nonzero and linearly dependent with $v$, we can characterize the same bijection $L_v \to L_{v'}$ via an auxiliary linearly independent $w$.

6. Fix an arbitrary $v \neq 0$ in $V$. The above constructions give us addition on $L_v$ and allow us to construct the multiplication map $L_v \times L_v \to L_v$ given by $(av, bv) \mapsto abv$. This assigns the structure of a field to $\mathbb L_v := L_v$. This field is, of course, isomorphic to $F$. The above observations allow us to define the vector space action of $\mathbb L_v$ on $V$.

7. The function $f$ must restrict to an isomorphism of fields $\mathbb L_v \to \mathbb L_{f(v)}$, and be linear with respect to this isomorphism. The isomorphism of fields need not necessarily agree with the map $av \mapsto af(v)$, which is why $f$ may not necessarily be linear.

Answer 2

See for instance my answer here. (I remember answering similar questions more than once, but maybe only in comments, which are not searchable.) In that answer I discuss the case of projective transformations while you are asking here about affine transformations, but the proof is the same. The idea, due to von Staudt (it appeared in his 1850 2-volume book on projective geometry), is to do "geometric algebra", i.e. to encode the binary algebraic operations in a field by certain point-line configurations. A good reference is "Foundations of Projective Geometry" by Robin Hartshorne. As for where the topology shows up: One can recover the topology of ${\mathbb R}$ from its ordered field structure which, in turn, can be recovered from pure algebra, as $x^2>0$ for all $x\ne 0$ and vice versa (every positive real number is a square). The situation is drastically different over other fields, e.g. over the complex numbers since one has to take into account the entire absolute Galois group which does not act continuously on ${\mathbb C}$.

The following is a configuration which describes the addition of real numbers.

An aside: The idea of "geometric algebra" goes back to the classical Greek mathematics (for them the entire algebra was geometric); it is still quite useful, some of the most spectacular applications are in the field of oriented matroids and convex polytopes (Mnev's universality theorem): Mnev was using the original von Staudt's configurations to prove his theorem.