This is Exercise 1.6.I from Vakil's notes on Algebraic Geometry.
Suppose $\mathscr{C}$ is an abelian category and $a: \mathscr{I}\rightarrow \mathscr{C}, b: \mathscr{I}\rightarrow \mathscr{C}$ are two diagrams in $\mathscr{C}$ indexed by $\mathscr{I}$. Let $A_i=a(i)$ and $B_i=b(i)$ be two objects in those diagrams. Let $h_{i}: A_{i}\rightarrow B_{i}$ be maps commuting with the maps in the diagram, i.e., $h_{i}$ is a natural transformation of functors $a\rightarrow b$. Then the $\ker h_i$ form another diagram in $\mathscr{C}$ indexed by $\mathscr{F}$. Describe a canonical isomorphism $\varprojlim \ker h_i\cong \ker (\varprojlim A_i\rightarrow \varprojlim B_i)$, assuming the limits exist.
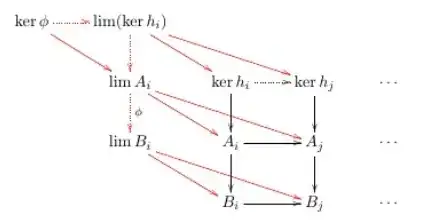
I showed the first part, which is illustrated using the following diagram.
I am trying to describe the isomorphism using the following diagram:
The dashed arrows are all due to the universal property. It remains to prove there exists a unique map from $\lim(\ker h_i)$ to $\ker h$ that makes the diagram commute. Then there exists a unique isomorphism between them.
My question:
To see that, it suffices to show that the map $\lim(\ker h_i)\rightarrow \lim A_i\rightarrow \lim B_i$ is zero. I am not sure how to. Is the following argument correct?
And it is zero since it is the unique map such that the square $\lim(\ker h_i)\rightarrow \ker h_i\rightarrow B_i$ and $\lim(\ker h_i)\rightarrow \lim A_i\rightarrow \lim B_i\rightarrow B_i$ commutes. The commutativity follows from Exercise 1.3.Q. Since one side is obviously zero, the unique map makes the other side zero must be zero.
Thank you for your help!