NFA to DFA conversion

Question

I am trying to convert the following NFA to an equivalent DFA:

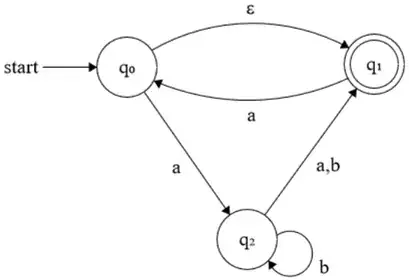
My steps:

1. There is an $\varepsilon$-transition from $q_0$ to $q_1$, hence the set of initial states is $\{q_0,q_1\}$.
2. From $\{q_0,q_1\}$ we can go to any state if the input is $a$, but get nowhere if the input is $b$, hence we will have the transitions $$\{q_0,q_1\}\overset{a}\longrightarrow\{q_0,q_1,q_2\} \textrm{ and }\{q_0,q_1\}\overset{b}\longrightarrow\text{Dead State}$$
3. From $\{q_0,q_1,q_2\}$ we can go to any state if the input is $a$ and get to $q_1$ or $q_2$ if the input is $b$, hence we will have the transitions $$\{q_0,q_1,q_2\}\overset{a}\longrightarrow\{q_0,q_1,q_2\} \textrm{ and } \{q_0,q_1,q_2\}\overset{b}\longrightarrow\{q_1,q_2\}$$
4. From $\{q_1,q_2\}$ we can go to $\{q_0,q_1\}$ if the input is $a$ and get to $q_1$ or $q_2$ if the input is $b$, hence we will have the transitions $$\{q_1,q_2\}\overset{a}\longrightarrow \{q_0,q_1\} \textrm{ and }\{q_1,q_2\}\overset{b}\longrightarrow \{q_1,q_2\}$$
5. Any state that includes $q_1$ is an accepting state.

Thus, my solution looks as follows:

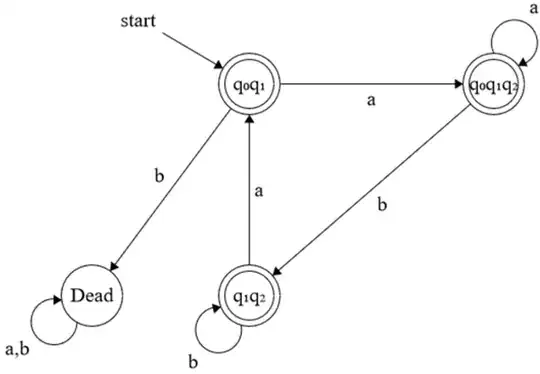
Is this correct?

Thanks in advance.