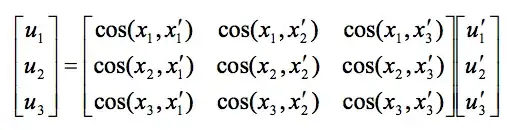11

I'm rotating points from one coordinate system to the other, but drawing a blank how to do this.

I've done some reading about Euler angles but after staring at this GIF for a while I just get dizzy.

enter image description here

above: from here

What I am doing:

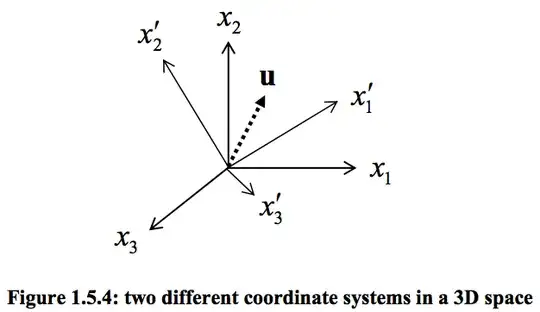
The new $z$ axis is perpendicular the plane containing the origin, $p_1$ and $p_2$, and the new $x$ axis goes through $p_1$. There is no change in origin.

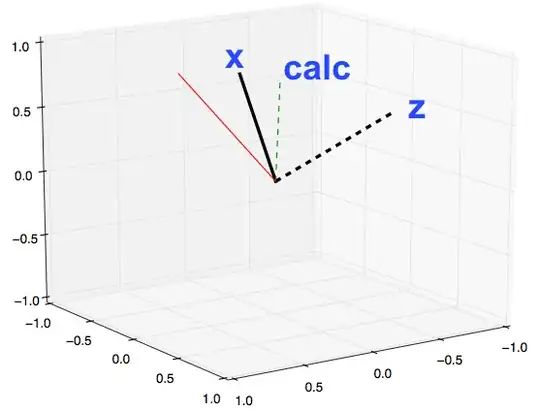
Looking for $p_{calc}$ in the rotated cartesian coordinates. Here is a plot of some normals. Math answer that's simple enough for me to re-write in python is fine.

edit: This PDF seems to be helpful.

enter image description here

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

p1    = np.array([-1489., -4913.,  4345.])
p2    = np.array([ 2633., -3268.,  5249.])
pcalc = np.array([-3210., -4390.,  3930.])

def normit(v):
    return v / np.sqrt((v**2).sum())

n1, n2, ncalc = [normit(p) for p in [p1, p2, pcalc]]

new_zaxis  = normit(np.cross(n1, n2))
new_xaxis  = n1
zero       = np.zeros(3) 

fig = plt.figure(figsize=[10, 8])
ax  = fig.add_subplot(1, 1, 1, projection='3d')

x, y, z = zip(zero, new_xaxis)
plt.plot(x, y, z, '-k', linewidth=3)

x, y, z = zip(zero, new_zaxis)
plt.plot(x, y, z, '--k', linewidth=3)

x, y, z = zip(zero, n2)
plt.plot(x, y, z, '-r', linewidth=1)

x, y, z = zip(zero, ncalc)
plt.plot(x, y, z, '--g', linewidth=1)

ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-1, 1)

plt.show()
uhoh
  • 1,967

2 Answers2

8

note: A nicer looking and correct answer will still get accepted, thanks!

I've read on page 27 here that a 3x3 transform matrix can be just the nine dot products - thank you U. Auckland's prof. Kelly!

enter image description here

enter image description here

above x2: screenshots from here.

Here is a very ugly implementation which seems to work. 

new_yaxis = -np.cross(new_xaxis, new_zaxis)

# new axes:
nnx, nny, nnz = new_xaxis, new_yaxis, new_zaxis
# old axes:
nox, noy, noz = np.array([1, 0, 0, 0, 1, 0, 0, 0, 1], dtype=float).reshape(3, -1)

# ulgiest rotation matrix you can imagine
top = [np.dot(nnx, n) for n in [nox, noy, noz]]
mid = [np.dot(nny, n) for n in [nox, noy, noz]]
bot = [np.dot(nnz, n) for n in [nox, noy, noz]]

def newit(vec):
    xn = sum([p*q for p,q in zip(top, vec)])
    yn = sum([p*q for p,q in zip(mid, vec)])
    zn = sum([p*q for p,q in zip(bot, vec)])
    return np.hstack((xn, yn, zn))

Let's see what happens...

nnx:         array([-0.22139284, -0.73049229,  0.64603887])
newit(nnx):  array([ 1.,  0.,  0.])

nny:         array([ 0.88747002,  0.1236673 ,  0.44396325])
newit(nny):  array([ 0.,  1.,  0.])

nnz:         array([-0.40420561,  0.67163042,  0.62091095])
newit(nnz:   array([ 0.,  0.,  1.])

OK then, this seems to be the right way to go.

uhoh
  • 1,967
3

Thank you uhoh for the math. Here is the same using np.inner

new_yaxis = -np.cross(new_xaxis, new_zaxis)

new axes:


new_axes  = np.array([new_xaxis, new_yaxis, new_zaxis])


old axes:


old_axes = np.array([1, 0, 0, 0, 1, 0, 0, 0, 1], dtype=float).reshape(3, -1)


rotation_matrix = np.inner(new_axes,old_axes)
#vec can be vectors Nx3
def newit(vec):
  return np.inner(vec,rotation_matrix)

And your test

new = newit(new_axes)
#new_axes:
[[-0.22139284 -0.73049229  0.64603887]
 [ 0.88747002  0.1236673   0.44396325]
 [-0.40420561  0.67163042  0.62091095]]
#new:
[[ 1.00000000e+00 -2.06024710e-17  6.10077552e-17]
 [-2.06024710e-17  1.00000000e+00  4.13972145e-17]
 [ 6.10077552e-17  4.13972145e-17  1.00000000e+00]]
Ynjxsjmh
  • 103
user822637
  • 31