How to calculate width and height of a 45° rotated ellipse bounded by a square?

Question

I'm coming from a programming background so I apologies if this is blindingly simple or I misuse terms. I have an ellipse bounded by a square. For simplicity the centre of the square and ellipse is the origin (0,0) while the square is 2 width and 2 height.

The ellipse is rotated -45° or +45° (angle in image) and I can easily work this out. The ellipse touches all sides of the square, and I also know the intersection points. In the image A is the distance between the corner and the intersection while B is the length of the long section (the other points are symmetric).

What is the width and height, as described in the image, of the ellipse?

Answer 1

Start with an ellipse with semi-axes $a\geq b$ in standard position, and intersect it with a $45^\circ$-line $x+y=s>0$, such that the two points of intersection coalesce. This is the case if $s=\sqrt{a^2+b^2}$, and for the point of tangency $(x_*,y_*)$ one obtains $x_*={a^2\over s}$, so that $s-x_*={b^2\over s}$.

In the case at hand the length $s=\sqrt{2}$ is given, and $${A\over B}={s-x_*\over x_*}={b^2\over a^2}\ .$$ We therefore have to solve the system $$a^2+b^2=2,\qquad {b^2\over a^2}={A\over B}$$ for $a$ and $b$. Since $A+B=2$ the result simplifies to $$a=\sqrt{B},\quad b=\sqrt{A}\ .$$

Answer 2

Suppose the ellipse's point of tangency $T$ with the square's top edge is $(k,1)$, where $-1\le k\le1$. ($k$ can be derived from $A$ or $B$ in the given diagram as $k=A-1=1-B$.) Now rotate the entire figure (square and ellipse) 45° clockwise about the origin; $T$'s new coordinates are $$\begin{bmatrix} \cos-45^\circ&-\sin-45^\circ\\ \sin-45^\circ&\cos-45^\circ\end{bmatrix}\begin{bmatrix}k\\1\end{bmatrix}=\frac{\sqrt2}2\begin{bmatrix}1&1\\-1&1\end{bmatrix}\begin{bmatrix}k\\1\end{bmatrix}=\frac{\sqrt2}2\begin{bmatrix}1+k\\1-k\end{bmatrix}$$

Given the ellipse's semi-axes $a$ and $b$ and a parameter $t$ as marked in the diagram above, the new $T$'s coordinates are also given by $(a\cos t,b\sin t)$. Equating the two representations of $T$ we have $$x=a\cos t=\frac{\sqrt2}2(1+k)$$ $$y=b\sin t=\frac{\sqrt2}2(1-k)$$ $$\frac ba\tan t=\frac{1-k}{1+k}\tag1$$ Taking derivatives with respect to $t$, we see that the tangent vector at $T$ is $(-a\sin t,b\cos t)$, so the slope at $T$ is $-\frac ba\cot t$, which is also $-1$ because it is parallel to the square's northeast face. Thus we find that $\tan t=\frac ba$, and substituting into $(1)$ we get $$\tan^2t=\frac{1-k}{1+k}$$ $\sin t$ and $\cos t$ can now be recovered: $$\cos t=\frac1{\sqrt{1+\tan^2t}}=\frac1{\sqrt{1+\frac{1-k}{1+k}}}=\frac1{\sqrt{\frac2{1+k}}}=\sqrt{\frac{1+k}2}$$ $$\sin t=\sqrt{1-\cos^2t}=\sqrt{1-\frac{1+k}2}=\sqrt{\frac{1-k}2}$$ Finally, the semi-axes $a$ and $b$ may be found as follows: $$a=\frac x{\cos t}=\frac{\frac{\sqrt2}2(1+k)}{\sqrt{\frac{1+k}2}}=\frac{\frac{\sqrt2}2(1+k)\sqrt2}{\sqrt{1+k}}=\sqrt{1+k}=\sqrt A=\sqrt{2-B}$$ $$b=\frac y{\sin t}=\frac{\frac{\sqrt2}2(1-k)}{\sqrt{\frac{1-k}2}}=\frac{\frac{\sqrt2}2(1-k)\sqrt2}{\sqrt{1-k}}=\sqrt{1-k}=\sqrt{2-A}=\sqrt B$$ The ellipse's width is $2a$ and its height is $2b$.

Answer 3

Consider an square formed by the sides of $\pm x\pm y=m$ (i.e. side length $m\sqrt2$).

Now find an ellipse which touches the square. Consider the top right quadrant. Edge of square is $$L: \quad x+y=m$$Assume point of tangency is $P(h,k)$.

Ellipse, $E$: $$\begin{align} \frac {x^2}{a^2}+\frac {y^2}{b^2}&=1\\ \frac {dy}{dx}&=-\frac {b^2x}{a^2y}=-\frac {b^2h}{a^2k}=-1\quad\text{at }P\\ \frac h{a^2}&=\frac k{b^2} \end{align}$$ $P$ lies on L, hence $h+k=m$, which gives $$\begin{align} h&=\left(\frac {m}{a^2+b^2}\right)a^2\\ k&=\left(\frac {m}{a^2+b^2}\right)b^2 \end{align}$$ $P$ lies on $E$, hence $$\begin{align} \left(\frac {m}{a^2+b^2}\right)^2\left[\frac {(a^2)^2}{a^2}+\frac {(b^2)^2}{b^2}\right]&=1\\ m&=\sqrt{a^2+b^2} \end{align}$$ This gives $$\begin{align} h&=\frac {a^2}m\\ k&=\frac {b^2}m\end{align}$$

$P$ divides edge of square into side lengths $$B=h\sqrt{2}=\frac {a^2\sqrt{2}}m\\ A=k\sqrt{2}=\frac {b^2\sqrt{2}}m$$ In the question posted, side length of square is $2$, hence $m=\sqrt{2}$, which gives $$A=b^2\\ B=a^2$$

"Height" (major axis) and "Width" (minor axis) of $E$ are given by

$$\text{Height (major axis)=}\color{red}{2a=2\sqrt{B}}\\ \text{Width (minor axis)=}\color{red}{2b=2\sqrt{A}}$$

---

Note

$\hspace{3cm}$

From this solution to another recent MSE question, note that the ellipse

$$\frac{x^2}{u}+\frac {y^2}{1-u}=1$$ has a nice property in that its point of tangency with the line $L: x+y=1$ is $(u,1-u)$ which divides the line segment $V(0,1), H(1,0)$ on $L$ in the ratio $u:1-u$. Note that $0<u<1$. The line segment $VH$ has length $\sqrt2$. The semi-major and semi-minor axes of the ellipse are $\sqrt{u}, \sqrt{1-u}$ respectively.

Answer 4

I arrive at the general formula for these ellipses (with your parameter $A$):

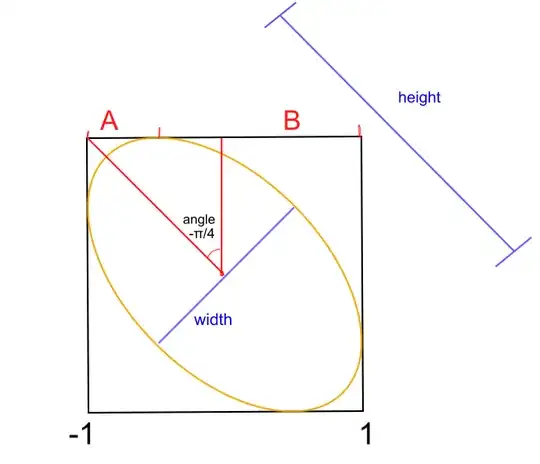
$\tag{0}\dfrac{(x + y)^2}{A} + \dfrac{(x - y)^2}{2-A}= 2$

with height=$\sqrt{A}$ and width=$\sqrt{2-A}$.

in a still different manner compared with @Christian Blatter and Parcly Taxel.

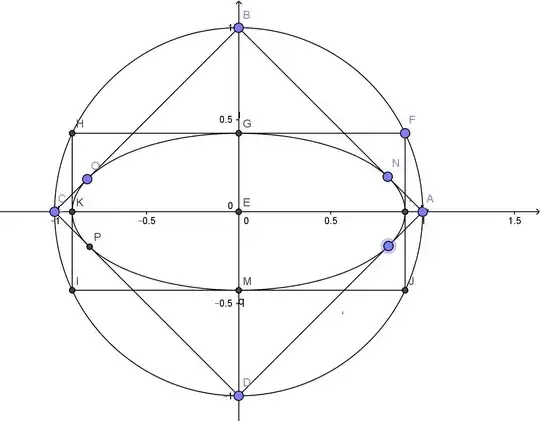
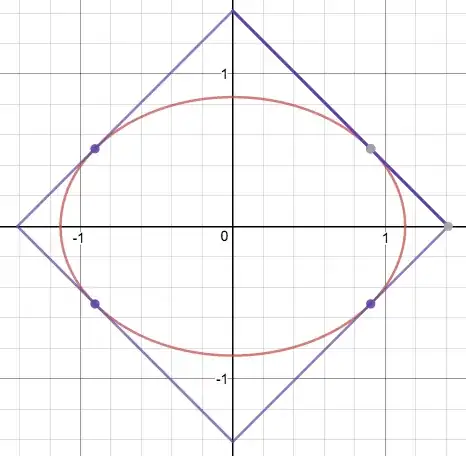
I first consider on the family $F$ of ellipses with axes $Ox$ and $Oy$ that are inscribed in the rotated square $C$ with vertices $(1,0), (0,1), (-1,0), (0,-1)$. (as Parcly Taxel does). It means that unit circle is their common "orthoptic circle": a theorem (established by Monge) says that the locus of points from which the 2 tangents that one can draw to the ellipse are orthogonal is a circle. See this. Remark : the name "orthoptic" comes from the fact that from any point of this circle, one "sees" the ellipse under a right angle.

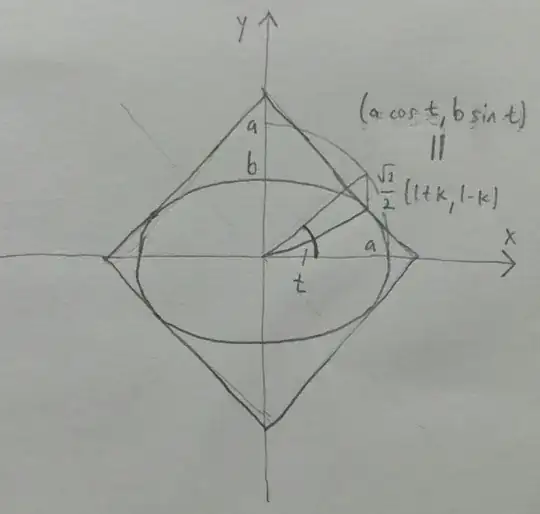
Thus, using this property for a given ellipse $E \in F$, the rectangle $R$ with sides parallel to the axes which is circumscribed to E is inscribed in the unit circle. It should be observed that ratio length/width for $R$ is the same as the ratio of semi-axes of E. The coordinates of the vertices of $R$ are $(\pm \cos(t),\pm \sin(t))$, for a certain $t$. Thus, setting $a:=\cos(t)$, we have $\sqrt{1-a^2}=\sin(t)$ and the general ellipse $E \in F$ has equation:

$$\tag{1}\dfrac{X^2}{a^2}+\dfrac{Y^2}{1-a^2}=1$$

Now, by using a $\pi/4$ rotation of coordinates associated with a $\sqrt{2}$ enlargement (homothety), i.e. transformation $\cases{X=x+y\\Y=x-y}$ (in order that square C is transformed into the desired square), we obtain:

$$\tag{2}\dfrac{(x+y)^2}{a^2}+\dfrac{(x-y)^2}{1-a^2}=4$$

It remains to express (2) with parameter $A$ instead of parameter $A$. This is easily done by imposing, that (2) is verified for point $(x,y)=(A-1,1)$. This gives $a^2=\dfrac{A}{2}$. Plugging this expression into (2), one obtains equation (0).

The height and width are deduced from equation (0) by computing the coordinates of points $(x,x)$ and $(-x,x)$ of the ellipse.